giải phương trình x2 - 9x+18=0

Những câu hỏi liên quan
Giải phương trình x 2 − 9 x + 20 = 0
Cách 1: x 2 − 9 x + 20 = 0
∆ =81-80=1>0 nên phương trình có hai nghiệm phân biệt x 1 = 9 + 1 2 = 5 ; x 2 = 9 − 1 2 = 4
Vậy phương trình có tập nghiệm S={4;5}
Cách 2:
x 2 − 9 x + 20 = 0 = 0 ⇔ x 2 − 5 x − 4 x + 20 = 0 ⇔ ( x − 5 ) ( x − 4 ) = 0 ⇔ x − 5 = 0 x − 4 = 0 ⇔ x = 5 x = 4
Vậy phương trình có tập nghiệm S={4;5}
Đúng 0
Bình luận (0)
Cho phương trình 2x2+9x-6=0 hai nghiệm x1,x2. Không giải phương trình, hãy tính giá trị của biểu thức B=4x12+4x22 +5x1*x2
Áp dụng Viét có: `{(x_1+x_2=-b/a=-9/2),(x_1.x_2=c/a=-3):}`
Ta có:`B=4(x_1 ^2+x_2 ^2)+5x_1.x_2`
`<=>B=4(x_1+x_2)^2-8x_1.x_2+5x_1.x_2`
`<=>B=4(-9/2)^2-3.(-3)`
`<=>B=90`
Đúng 0
Bình luận (0)
không giải phương trình, hãy tính: x2 + 9x - 13 = 0 thỏa mãn:
x12x2 + x1x22
Ta có:\(\Delta=9^2-4.1.\left(-13\right)=81+52=133>0\)
\(\Rightarrow\) Pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-9\\x_1x_2=-13\end{matrix}\right.\)
\(x^2_1x_2+x_1x^2_2=x_1x_2\left(x_1+x_2\right)=\left(-13\right)\left(-9\right)=117\)
Đúng 3
Bình luận (0)
Giải bất phương trình
g
(
x
)
≤
0
với
g
(
x
)
x
2
+
3
x
−
9
x
−
2
A. S (1; 3) B.
S
...
Đọc tiếp
Giải bất phương trình g ' ( x ) ≤ 0 với g ( x ) = x 2 + 3 x − 9 x − 2
A. S = (1; 3)
B. S = 1 ; 3 / 2
C. S = − ∞ ; 1 ∪ ( 3 ; + ∞ )
D. S = − ∞ ; 1
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B
Đúng 0
Bình luận (0)
Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình 2 x 2 + 9x + 7 = 0
2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
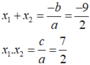
Đúng 0
Bình luận (0)
10: Giải phương trình :5√2x−8−2√9x−18=0
- Giải phương trình sau: 5/3 * sqrt(9x - 18) - 1/2 * sqrt(16) overline 6x-32 -15=0
Giải các pt sau:
a) 3X2 + 8X + 4 = 0
b) X2 + 9X + 18 = 0
c) X2 + 12 + 32 = 0
a) \(\text{Δ}=8^2-4.3.4=16\)
\(\left[{}\begin{matrix}x=\dfrac{-8+4}{2.3}=-\dfrac{2}{3}\\x=\dfrac{-8-4}{2.3}=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
b) \(\text{Δ}=9^2-4.1.18=9\)
\(\left[{}\begin{matrix}x=\dfrac{-9+3}{2}=-3\\x=\dfrac{-9-3}{2}=-6\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c) \(x^2+12+32=0\)
\(x^2=-44\)
mà \(x^2\ge0\forall x\)
\(\Rightarrow\) pt vô nghiệm
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình và bất phương trình sau
x^2( - 2) - 9x = - 18
7/ 1-2x bé thua hoặc bằng 0
x^2( - 2) - 9x = - 18
<=>-2x2-9x=-18
=>-2x2-9x+18=0
(-9)2-(-4(2.18))=225
\(x_{1,2}=\frac{-b\pm\sqrt{\Delta}}{2a}=-\frac{9\pm\sqrt{225}}{4}\)
x1=-6;x2=\(\frac{3}{2}\)
Đúng 0
Bình luận (0)
\(a.\) \(x^2\left(-2\right)-9x=-18\)
\(\Leftrightarrow\) \(2x^2+9x=18\)
\(\Leftrightarrow\) \(2x^2+9x-18=0\)
\(\Leftrightarrow\) \(2x^2-3x+12x-18=0\)
\(\Leftrightarrow\) \(x\left(2x-3\right)+6\left(2x-3\right)=0\)
\(\Leftrightarrow\) \(\left(2x-3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\) \(2x-3=0\) hoặc \(x+6=0\)
\(\Leftrightarrow\) \(x=\frac{3}{2}\) hoặc \(x=-6\)
Vậy, tập nghiệm của pt trên là \(S=\left\{-6;\frac{3}{2}\right\}\)
\(b.\)
Điều kiện để phương trình có nghĩa là \(x\ne\frac{1}{2}\)
Với điều kiện trên thì phương trình đã cho tương đương với:
\(\frac{7}{1-2x}\le0\) \(\Leftrightarrow\) \(1-2x\le0\) \(\Leftrightarrow\) \(1\le2x\) \(\Leftrightarrow\) \(x\ge\frac{1}{2}\)
Để thỏa mãn điều kiện xác định thì \(x>\frac{1}{2}\) (vì khi \(x=\frac{1}{2}\) thì mẫu thức bằng \(0\) nên phương trình không thể thực hiện được)
Kết luận: \(S=\left\{x\in R\text{|}x>\frac{1}{2}\right\}\)
Đúng 0
Bình luận (0)
a/ x2.(-2) - 9x = -18
=> -2x2 - 9x + 18 = 0
=> 2x2 + 9x - 18 = 0
=> 2x2 + 12x - 3x - 18 = 0
=> 2x.(x + 6) - 3(x + 6) = 0
=> (x + 6).(2x - 3) = 0
=> x + 6 = 0 => x = -6
hoặc 2x - 3 = 0 => x = 3/2
Vậy x = {6;3/2}
b/ \(\frac{7}{1-2x}<0\) Có: 7 > 0 . Để \(\frac{7}{1-2x}<0\) thì 1 - 2x < 0 => -2x < -1 => x > 1/2
Vậy x > 1/2 thì thỏa đề (câu này bạn ghi sai đề rồi nha, không có trường hợp biểu thức = 0 nha bạn)
Đúng 0
Bình luận (0)


















