cho hình lập phương ABCD.A'B'C'D'. Xác định góc giữa 2 đường thẳng
a) AB và B'C'
b) AC và B'C'
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh đường thẳng BC' vuông góc với mặt phẳng (A'B'CD)
b) Xác định và tính độ dài đoạn vuông góc chung của AB' và B'C
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD' và B'C.
b) Tính khoảng cách của hai đường thẳng BD' và B'C
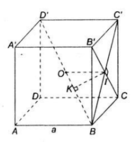
a) Ta có:
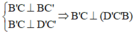
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
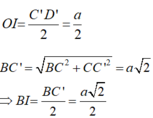
Vì ΔIOB vuông tại I có đường cao IK nên:
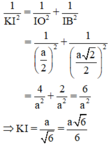
Bài 1. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 4. a. Tính độ dài đường chéo của hình lập phương. b. Tính góc giữa AC' và mặt đáy c. Tính góc giữa AC và B'C' d. Tính khoảng cách từ A đến (A'BD)
Cho hình lập phương ABCD.A'B'C'D'. Gọi M,N lần lượt là trung điểm của AB, B'C'. Góc giữa hai đường thẳng DM và A'N bằng A. 90° B. 60° C. 45° D. 30°
\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60 0
B. 90 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60
B. 90
C. 30
D. 45
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
![]()
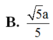
![]()
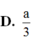
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B'D' bằng
A. a 5
B. a 5 5
C. 3 a
D. a 3
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên).
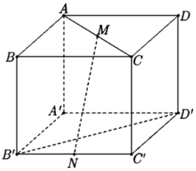
Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
A. a 5
B. 5 a 5
C. 3 a
D. a 3
Cho hình lập phương ABCD.A'B'C'D' các trung điểm E, F của các cạnh AB, DD'. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC') và (EFK) với K là trung điểm của cạnh B'C'.
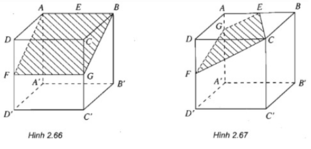
Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
- Mặt phẳng (EFB): ta vẽ FG //AB và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC'.
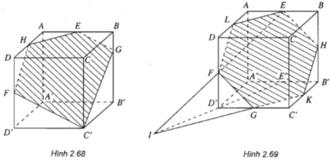
- (h.2.67) Mặt phẳng (EFC): Nối FC và vẽ EG // FC, ta được thiết diện là hình thang ECFG
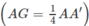
- (h.2.68) Mặt phẳng (EFC'): Nối FC' và vẽ EG // FC′. Nối GC' và vẽ FH // GC′. Ta được thiết diện là hình ngũ giác EGC'FH.
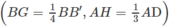
- (h.2.69) Mặt phẳng (EFK) với K là trung điểm của đoạn B'C'. Lấy trung điểm E' của đoạn A'B'. Ta có I = EF ∩ E′D. Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A'B'C'D'). Gọi G = IK ∩ C′D′. Nối F với G, vẽ EH // FG. Nối K với H, vẽ FL // KH và nối L với E. Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D'C', B'B, AD).