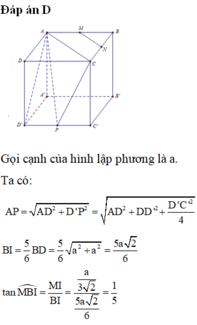
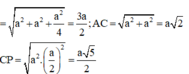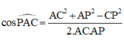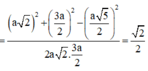Các câu hỏi tương tự
Cho hình lập phương ABCD.ABCD Gọi E. F lần lượt là trung điểm các cạnh BC, CD Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D Gọi E. F lần lượt là trung điểm các cạnh B'C', C'D' Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
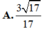
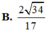
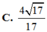
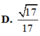
cho hình lập phương ABCD.A'B'C'D' và M,N,E,F lần lượt là trung điểm các cạnh BC, BA, AA' , A'D'. Tính góc giữa các cặp đường thẳng sau
a) A'C' và BC
b) MN và EF
c) MN và BC
d) EF và CC'
Cho hình hộp chữ nhật ABCD.ABCD có AB 4, AD 5, AA 6. Gọi M, N, P lần lượt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB =4, AD = 5, AA' =6. Gọi M, N, P lần lượt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
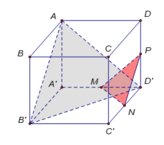
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Cho tứ diện ABCD có AB CD a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng
30
0
A. MN
a
2
B. MN
a
3
2
C. MN
a
3
3...
Đọc tiếp
Cho tứ diện ABCD có AB = CD =a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 0
A. MN = a 2
B. MN = a 3 2
C. MN = a 3 3
D. MN = a 4
Cho hình hộp chữ nhật ABCD.ABCD có AB4 AD 5 AA6 . Gọi M , N , P lần luợt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và bằng (MNP) A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4 AD =5 AA'=6 . Gọi M , N , P lần luợt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và bằng (MNP)
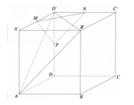
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng A.
1
3
B.
5
3
C.
2
3
D....
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
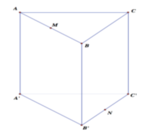
A. 1 3
B. 5 3
C. 2 3
D. 5 5
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
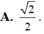
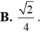
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’cạnh a. Gọi M, N lần lượt là trung điểm của AB, BC. Tính góc của cặp đường thẳng MN và C’D’ A. 30º B. 45º C. 60º D. 90º
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’cạnh a. Gọi M, N lần lượt là trung điểm của AB, BC. Tính góc của cặp đường thẳng MN và C’D’
A. 30º
B. 45º
C. 60º
D. 90º
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Côsin góc giữa hai đường thẳng MN và AC bằng A.
1
3
B.
2
3
C.
5
3
D.
5
5
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm các cạnh AB, B'C'. Côsin góc giữa hai đường thẳng MN và AC bằng
A. 1 3
B. 2 3
C. 5 3
D. 5 5