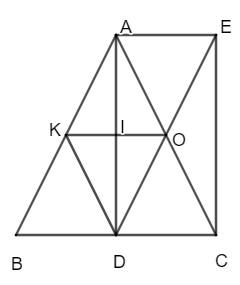
Câu 4: Cho tam giác ABC cân tại A đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua cạnh OA.
a. Chứng minh tứ giác ADCE là hình chữ nhật
b. Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE
c. cho AB = 10 cm BC = 12 cm. Tính diện tích tam giác OAB
d. đường thẳng Oy cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân
CỨu