x⁴ - 4x² + 12x - 9 = 0

<=> x⁴ - x³ + x³ - x² - 3x² + 3x + 9x - 9 = 0

<=> x³(x - 1) + x²(x - 1) - 3x(x - 1) + 9(x - 1) = 0

<=> (x - 1)(x³ + x² - 3x + 9) = 0

<=> (x - 1)(x³ + 3x² - 2x² - 6x + 3x + 9) = 0

<=> (x - 1)[ x²(x + 3) - 2x(x + 3) + 3(x + 3) ] = 0

<=> (x - 1)(x + 3)(x² - 2x + 3) = 0

<=> (x - 1)(x + 3)(x² - 2x + 1 + 2) = 0

<=> (x - 1)(x + 3)[ (x - 1)² + 2 ] = 0

<=> (x - 1)(x + 3) = 0 --> do (x - 1)² + 2 > 0 với mọi x

<=>

[ x - 1 = 0 =>[ x = 1

[ x + 3 = 0 =>[ x = -3

Bạn nên sửa >= là = vì giải bất phương trình mà

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(3-x\right)\left(3+x\right)}>0\)

Bảng xét dấu:

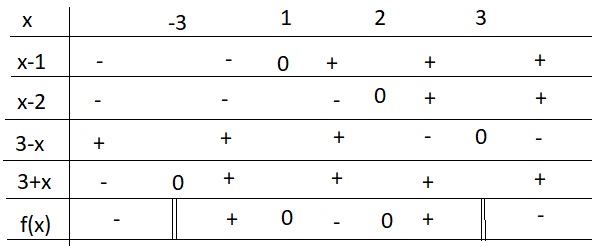
Từ bảng xét dấu ta có nghiệm của BPT là: \(x\in\left(-3;1\right)\cup\left(2;3\right)\)

Mấy bài này đều là toán lớp 8 mà. Mình mới lớp 8 mà cũng làm được nữa là bạn lớp 9 mà không làm được afk?

a) (3x - 2)(4x + 5) = 0

⇔ 3x - 2 = 0 hoặc 4x + 5 = 0

1) 3x - 2 = 0 ⇔ 3x = 2 ⇔ x = 2/3

2) 4x + 5 = 0 ⇔ 4x = -5 ⇔ x = -5/4

Vậy phương trình có tập nghiệm S = {2/3;−5/4}

b) (2,3x - 6,9)(0,1x + 2) = 0

⇔ 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0

1) 2,3x - 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3

2) 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.

Vậy phương trình có tập hợp nghiệm S = {3;-20}

c) (4x + 2)(x² +  1) = 0 ⇔ 4x + 2 = 0 hoặc x² +  1 = 0

1) 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = −1/2

2) x² +  1 = 0 ⇔ x² = -1 (vô lí vì x² ≥ 0)

Vậy phương trình có tập hợp nghiệm S = {−1/2}

d) (2x + 7)(x - 5)(5x + 1) = 0

⇔ 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0

1) 2x + 7 = 0 ⇔ 2x = -7 ⇔ x = −7/2

2) x - 5 = 0 ⇔ x = 5

3) 5x + 1 = 0 ⇔ 5x = -1 ⇔ x = −1/5

Vậy phương trình có tập nghiệm là S = {−7/2;5;−1/5}

a) x³ + 4x² - 29x + 24 = 0

<=> x³ - x² + 5x² - 5x - 24x + 24 = 0

<=> x²(x - 1) + 5x(x - 1) - 24(x - 1) = 0

<=> (x - 1)(x² + 5x - 24) = 0

\(\Leftrightarrow\left[\begin{matrix}x-1=0\\x^2+5x-24=0\end{matrix}\right.\)

+) x - 1 = 0 <=> x = 1

+) x² + 5x - 24 = 0

\(\Delta=5^2+4.1.24=121\Rightarrow\sqrt{\Delta}=11\)

Phương trình có 2 nghiệm phân biệt: \(x_1=\frac{-5+11}{2}=3;x_2=\frac{-5-11}{2}=-8\)

Vậy ...

a. pt <=> x³+5x²-24x-x²-5x+24 =0

<=> x(x²+5x-24)-(x²+5x-24)=0

<=> (x-1)(x²+5x-24)=0

<=> \(\left[\begin{matrix}x=1\\x=3\\x=-8\end{matrix}\right.\)

9) Dễ thấy phương trình không có nghiệm x = 0

Chia cả 2 vế của pt cho x² (x² \(\ne\) 0) ta được:

x² + x - 10 + \(\frac{1}{x}+\frac{1}{x^2}\) = 0

\(\Leftrightarrow\left(x+\frac{1}{x}\right)^2+\left(x+\frac{1}{x}\right)-12=0\) (1)

Đặt x + \(\frac{1}{x}\)= y

Thay vào (1) ta được: y² + y - 12 = 0

\(\Delta=1^2-4.1.\left(-12\right)=49\Rightarrow\sqrt{\Delta}=7\)

Phương trình có 2 nghiệm phân biệt: \(y_1=\frac{-1+7}{2}=3;y_2=\frac{-1-7}{2}=-4\)

+) y = x + \(\frac{1}{x}=3\)

\(\Leftrightarrow x=\frac{3+\sqrt{5}}{2};x=\frac{3-\sqrt{5}}{2}\)

+) y = x + \(\frac{1}{x}\) = -4

\(\Leftrightarrow x=-2+\sqrt{3};x=-2-\sqrt{3}\)

Vậy ...

toán lp 1 ???

toán lớp 1 sao học ghê vậy lm đc cả x vs ^ luôn ô mai gi gứ chóp bạn nào lớp 1 mà giải đc bài này luôn ?????

a/ \(\Leftrightarrow x^2-6x+9< 0\)

\(\Leftrightarrow\left(x-3\right)^2< 0\)

BPT vô nghiệm

b/ \(\Leftrightarrow12x^2-3x+1>0\)

\(\Leftrightarrow12\left(x-\frac{1}{8}\right)^2+\frac{13}{16}>0\) (luôn đúng)

Vậy tập nghiệm của BPT là \(D=R\)

c/ \(\Leftrightarrow2\left(x-4\right)\left(x-1\right)\left(x-3\right)>0\)

\(\Rightarrow\left[{}\begin{matrix}1< x< 3\\x>4\end{matrix}\right.\)

`x^2+2x+3>2`

`<=>x^2+2x+1>0`

`<=>(x+1)^2>0`

`<=>x+1 ne 0`

`<=>x ne -1`

`(x+5)(3x^2+2)>0`

Vì `3x^2+2>=2>0`

`=>x+5>0<=>x>-5`

c) Ta có: \(21x-10x^2+9< 0\)

\(\Leftrightarrow10x^2-21x-9>0\)

\(\Leftrightarrow x^2-\dfrac{21}{10}x-\dfrac{9}{10}>0\)

\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{21}{20}+\dfrac{441}{400}>\dfrac{801}{400}\)

\(\Leftrightarrow\left(x-\dfrac{21}{20}\right)^2>\dfrac{801}{400}\)

\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{3\sqrt{89}+21}{20}\\x< \dfrac{-3\sqrt{89}+21}{20}\end{matrix}\right.\)