(d):y=(m+1)x+3, (d'):y=2x+3
tìm tọa độ giao điểm của (d) và (d')
Vẽ (d) : y= x+3
(d') : y = -2x-3
Tìm tọa độ giao điểm bằng ptoán
PT hoành độ giao điểm: \(x+3=-2x-3\Leftrightarrow x=-2\Leftrightarrow y=1\Leftrightarrow A\left(-2;1\right)\)
Vậy \(A\left(-2;1\right)\) là giao điểm 2 đths
1/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -2x + 3 b) (P) : y = x² c) Tìm tọa độ giao điểm của hai đồ thị 2/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -x + 3 b) (P) : y = 2x² c) Tìm tọa độ giao điểm của hai đồ thị 3/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= x - 3 b) (P) : y = -3x² c) Tìm tọa độ giao điểm của hai đồ thị
1:
a: 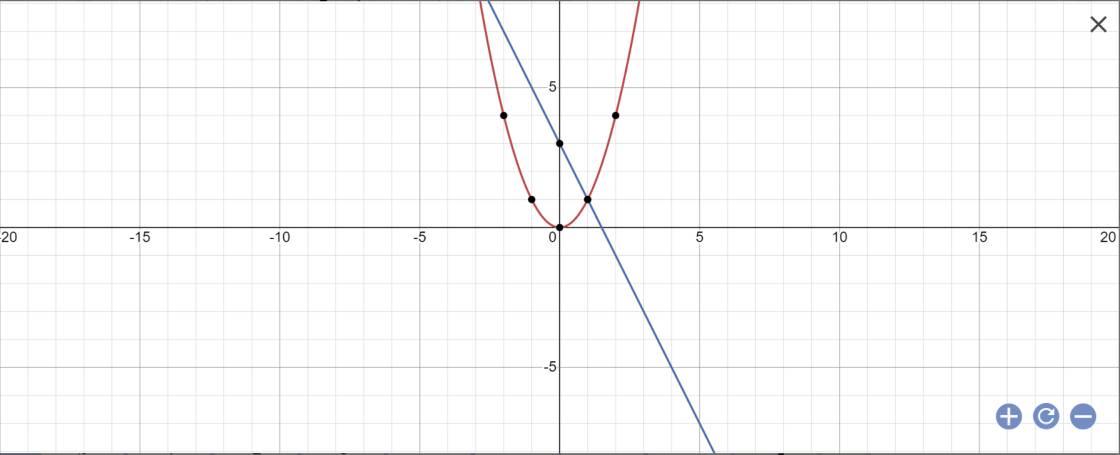
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1
Cho (D) : y = 2x – 5 và (D’) : y = – 1 2 x. a/ Vẽ (D) và (D’) trên cùng 1 mặt phẳng tọa độ. b/ Tìm tọa độ giao điểm M của (D) và (D’) bằng phép tính.
\(b,\text{PT hoành độ giao điểm: }2x-5=-\dfrac{1}{2}x\Leftrightarrow\dfrac{5}{2}x=5\Leftrightarrow x=2\Leftrightarrow y=-1\Leftrightarrow M\left(2;-1\right)\)
cho hàm số y=x-3(d) và y=2x+1(d') a)vẽ (d) và (d)' trên cùng một mặt phẳng tọa độ Oxy b)gọi M là giao điểm (d) và (d') tìm tọa độ M
cho hàm số y=x-3(d) và y=2x+1(d') a)vẽ (d) và (d)' trên cùng một mặt phẳng tọa độ Oxy b)gọi M là giao điểm (d) và (d') tìm tọa độ M
b. PT hoành độ giao điểm \(x-3=2x+1\Leftrightarrow x=-4\Leftrightarrow y=-7\Leftrightarrow M\left(-4;-7\right)\)
Vẽ (d) và (d’) và tìm tọa độ giao điểm của (d) và (d’)
(d): y= -2x+3 và (d’):y=1/2x-3
PT hoành độ giao điểm: \(-2x+3=\dfrac{1}{2}x-3\Leftrightarrow\dfrac{5}{2}x=6\Leftrightarrow x=\dfrac{12}{5}\Leftrightarrow y=-\dfrac{9}{5}\Leftrightarrow A\left(\dfrac{12}{5};-\dfrac{9}{5}\right)\)
Vậy \(A\left(\dfrac{12}{5};-\dfrac{9}{5}\right)\) là giao điểm 2 đths
trong ngoài tọa độ Oxy ch parabol (P): y=x^2/2 và (d): y=(m+1)x+m-3
tìm m: a) để (d) ko cắt (P)
b)) (d) cắt (P) tại 2 điểm phân biệt
c) (d) tiếp xúc (P)
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2-\left(m+1\right)x-m+3=0\)
\(\Leftrightarrow x^2-\left(2m+2\right)x-2m+6=0\)
\(\text{Δ}=\left(2m+2\right)^2-4\left(-2m+6\right)\)
\(=4m^2+8m+4+8m-24\)
\(=4m^2+16m-20\)
\(=4\left(m^2+4m-5\right)\)
\(=4\left(m+5\right)\left(m-1\right)\)
a: Để (P) không cắt (d) thì (m+5)(m-1)<0
hay -5<m<1
b: Để (P) cắt (d) tại hai điểm phân biệt thì (m+5)(m-1)>0
=>m>1 hoặc m<-5
c: Để (P) tiếp xúc với (d) thi (m+5)(m-1)=0
=>m=-5 hoặc m=1
(P):y=x2 (d):y=2x+m
a)Vẽ (P)và (d)trên cùng 1 hệ trục tọa độ với m=3 và tìm tọa độ giao điểm của (P) và (d) (mk ko cần hình vẽ đâu)
b)Tìm m để (d) tiếp xúc với (P) .Tìm tọa độ tiếp điểm
a: Khi m=3 thì (d): y=2x+3
Phương trình hoành độ giao điểm là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Khi x=3 thì y=9
Khi x=-1 thì y=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x-m=0\)
Δ=4+4m
Để (P) tiếp xúc với (d) thì 4m+4=0
hay m=-1
Cho hàn số (d): y= 2x+3
a) Tìm tọa độ giao điểm của (d) với trục hoành và trục tung
b) Tìm giá trị của m đển (d'): y= (m-1)x + 3 vuông góc với (d)
Lời giải:
Gọi tọa độ giao điểm của $(d)$ với trục hoành là $(a,0)$.
Vì $(a,0)\in (d)$ nên: $0=2.a+3\Rightarrow a=\frac{-3}{2}$
Vậy $(\frac{-3}{2},0)$ là giao điểm của $(d)$ với trục hoành.
Gọi tọa độ giao điểm của $(d)$ với trục tung là $(0,b)$.
$(0,b)\in (d)$ nên: $b=2.0+3=3$. Vậy $(0,3)$ là giao của $(d)$ với trục tung
b)
Để $(d')$ vuông góc với $(d)$ thì:
$2(m-1)=-1\Leftrightarrow m=\frac{1}{2}$