dễ thế mà ko biết

B=1x1+2x2x1+3x3x1+.......+nxnx1

B=1+4+9+........+nxn

B=1+4+9+......+2n

vì mỗi lần cách thì tăng thêm 1 đơn vị vậy

Ta có A = 1x(2-1) + 2x(3-1)+3x(4-1)+...+nx(n+1 - 1) Hay A = 1x2+2x3+3x4+...+nx(n+1)-(1+2+3+...+n) tách ra làm hai dãy thì hai dãy

B = 1x2+2x3+3x4+...+nx(n+1) (dãy này ra nx(n+1)x(n+2)/3) và

C = 1+2+3+..+n ra nx(n+1)/2 trừ đi là ra kết quả

Ta có A = 1x(2-1) + 2x(3-1)+3x(4-1)+...+nx(n+1 - 1) Hay A = 1x2+2x3+3x4+...+nx(n+1)-(1+2+3+...+n) tách ra làm hai dãy thì hai dãy B = 1x2+2x3+3x4+...+nx(n+1) (dãy này ra nx(n+1)x(n+2)/3) và C = 1+2+3+..+n ra nx(n+1)/2 trừ đi là ra kết quả

Câu 7. Sắp xếp các hạng tử của đa thức

giảm dần của biến.

P(x) = 10 - 4x⁴ + 3x³ - 2x² + x

theo lũy thừa giảm

A. P(x) = 10 + x - 2x² + 3x³ - 4x⁴ .                      B.

C. P(x) = -4x⁴ - 2x² + 3x³ + x +10 .                    D.

P(x) = -4x⁴ + 3x³ - 2x² + x +10 .

P(x) = 3x³ + x +10 - 2x² - 4x⁴ .

Câu 8. Sắp xếp các hạng tử của đa thức

tăng dần của biến.

P(x) = 3x² -10 + 2x³ + 4x + x⁴

theo lũy thừa

A. P(x) = -10 + x⁴ + 2x³ + 3x² .                            B.

C. P(x) = -10 + 4x + 3x² + 2x³ + x⁴ .                    D.

P(x) = x⁴ + 2x³ + 3x² + 4x -10 .

P(x) = x⁴ + 3x² + 2x³ + 4x -10 .

Câu 9. Bậc của đơn thức 3y2 (2y2 )3 y là

A. 6 .                                B. 7 .                                 C. 8 .                                 D. 9 .

Câu 10. Hệ số cao nhất của

P(x) = x⁴ + 3x² + 2x³ + 4x -10 là

A. 1 .                                 B. 3 .                                 C. 4 .                                 D.

-10 .

Câu 11. Thu gọn đa thức x3 - 5y2 + x + x3 - y2 - x ta được

A.  x6  - 6y4 .                    B.

x6  - 4y4 .                    C.

2x3  - 6y2 .                   D. 2x3 - 4y2 .

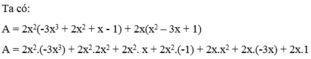
A   = − 6 x 5 + 4 x 4 + 2 x 3 − 2 x 2 + 2 x 3 − 6 x 2 + 2 x

A   =   − 6 x 5 + 4 x 4 + 4 x 3 − 8 x 2 + 2 x

Chọn đáp án C

2870 ĐÚNG NHÉ BẠN !

\(C=1x\left(2-1\right)+2x\left(3-1\right)+3x\left(4-1\right)+...+20x\left(21-1\right)\)

\(=1x2-1+2x3-2+3x4-3+...+20x21-20\)

\(=\left(1x2+2x3+3x4+...+20x21\right)-\left(1+2+3+...+20\right)\)

\(A=1x2+2x3+3x4+...+21x21\)

\(3xA=1x2x3+2x3x3+3x4x3+...+20x21x3\)

\(3xA=1x2x3+2x3x\left(4-1\right)+3x4x\left(5-2\right)+...+20x21x\left(22-19\right)\)

\(3xA=1x2x3-1x2x3+2x3x4-2x3x4+3x4x5-...-19x20x21+20x21x22\)

\(3xA=20x21x22\Rightarrow A=20x7x22=3080\)

\(B=1+2+3+...+20=\frac{20x\left(1+20\right)}{2}=210\)

\(C=A-B=3080-210=2870\)

Bài làm:

\(1+2.2+3.3+...+20.20\)

\(=1.\left(2-1\right)+2\left(3-1\right)+3\left(4-1\right)+...+20\left(21-1\right)\)

\(=1.2-1+2.3-2+3.4-3+...+20.21-20\)

\(=\left(1.2+2.3+3.4+...+20.21\right)-\left(1+2+3+...+20\right)\)

\(=\frac{1}{3}\left(1.2.3+2.3.3+...+20.21.3\right)-\frac{\left(20+1\right).20}{2}\)

\(=\frac{1}{3}\left[1.2.3+2.3.\left(4-1\right)+...+20.21.\left(22-19\right)\right]-210\)

\(=\frac{1}{3}\left(1.2.3-1.2.3+2.3.4-...-19.20.21+20.21.22\right)-210\)

\(=\frac{1}{3}.20.21.22-210\)

\(=3080-210\)

\(=2870\)

Học tốt!!!!

\(\left(2x^2-\dfrac{1}{3}xy+y^2\right)\left(-3x^3\right)=-6x^5+x^4y-3x^3y^2\)