Cứu e vs mng ưiiiiiii
ƯC(-14,28)
Cứu em vs mng
a) Cấu hình e của R: 1s22s22p63s1
b) R thuộc chu kì 3, nhóm IA, nguyên tố s
c) Do R có 1e lớp ngoài cùng => R có tính chất của kim loại
d) Cấu hình của X: 1s22s22p5
=> X là F(Flo)
cứu mik vs mng oii:((
Có một thanh thẳng, người ta nghi ngờ nó là thanh nam châm vĩnh cửu. làm cách nào để kiểm tra?
Hicc mng cứu e vs, mai thi r ạ ![]()
Để kiểm tra xem thanh thẳng có phải là thanh nam châm vĩnh cửu hay không, bạn có thể sử dụng một nam châm khác để thử nghiệm. Nếu thanh thẳng được hút hoặc bị đẩy bởi nam châm khác mà không cần phải tiếp xúc trực tiếp, có thể xác định được rằng nó là thanh nam châm vĩnh cửu.
1. Sử dụng một nam châm khác để tiếp xúc với thanh thẳng. Nếu hai nam châm hút lẫn nhau, có thể kết luận thanh thẳng là thanh nam châm vĩnh cửu.
2. Di chuyển thanh thẳng gần một vật kim loại như sắt. Nếu thanh thẳng hút vật kim loại, đó là một dấu hiệu cho thấy nó là thanh nam châm vĩnh cửu.
3. Đặt thanh thẳng vào một cuvet chứa nước. Nếu thanh thẳng chuyển động hoặc dao động trong nước, có thể chứng minh nó là thanh nam châm vĩnh cửu.
4. Kiểm tra tính nam châm của thanh thẳng bằng cách đặt một kim loại như sắt gần nó. Nếu kim loại bị hút lên bởi thanh thẳng, có thể xác định nó là thanh nam châm vĩnh cửu.
5. Nếu không thể xác định được bằng các phương pháp trên, có thể sử dụng thiết bị đo từ trường để kiểm tra mức độ từ trường của thanh thẳng. Nếu mức độ từ trường không thay đổi theo thời gian, có thể kết luận nó là thanh nam châm vĩnh cửu.
mng ơi cứu e vớiii !!!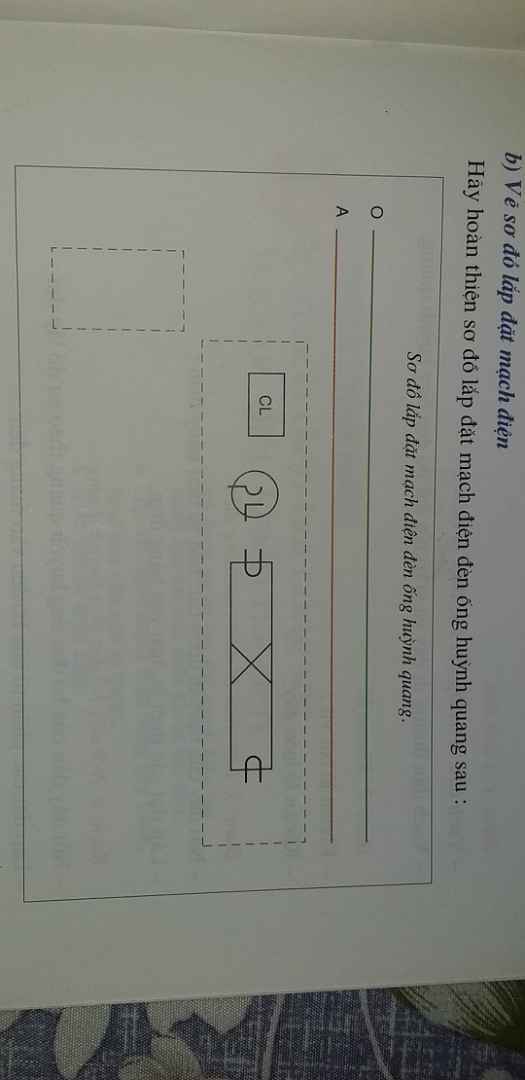
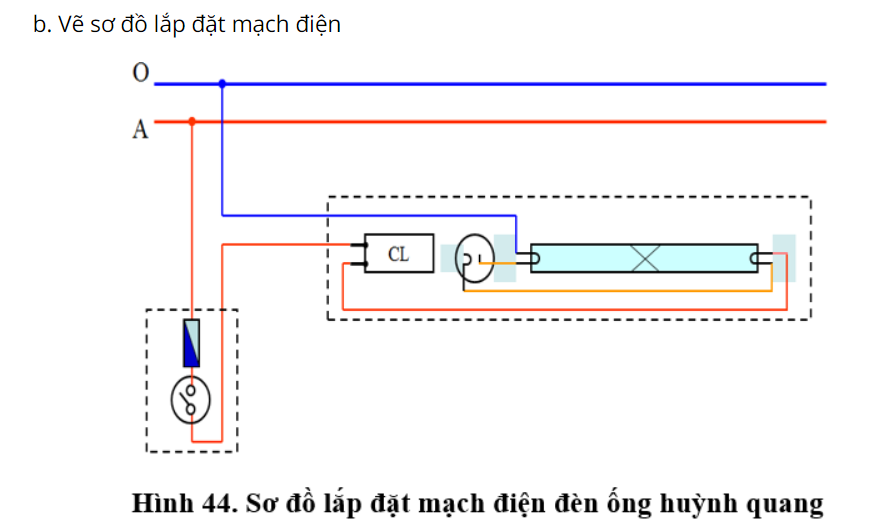
Nguồn: https://vietjack.com/giai-bai-tap-cong-nghe-9/ly-thuyet-thuc-hanh-lap-mach-dien-den-ong-huynh-quang.jsp
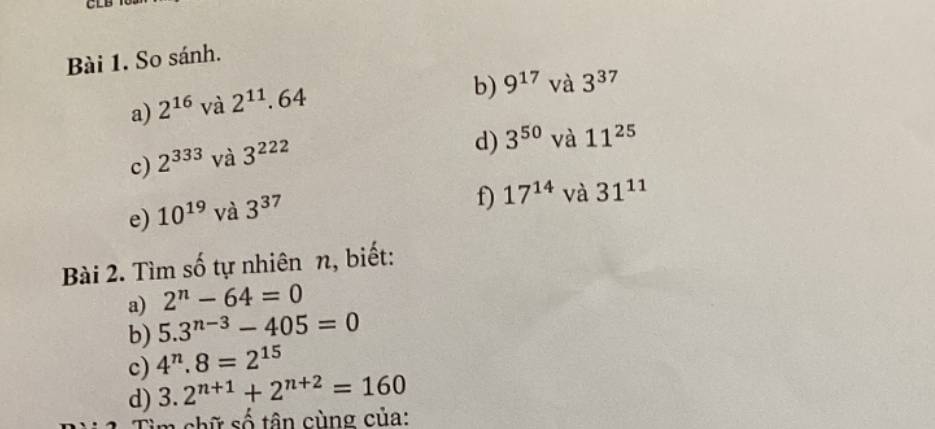
giúp e mng ooiiii, cứu e ạ huhu help mee
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)
Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Mng ơi cứu e gấp vớiii !!!
cứu e với mng🥹🥹
a: R1//R2
=>I=I1+I2=1,6(A)
b: R tđ=11,2/1,6=7(\(\Omega\))
\(a)I=I_1+I_2=0,5+1,1=1,6A\\ b)R_{tđ}=\dfrac{U}{I}=\dfrac{11,2}{1,6}=7\Omega\)

cứu e mng huhuhhuuh help me help me e sắp học r
3:
a: 5^n luôn có chữ số tận cùng là 5 với mọi n là số tự nhiên
=>5^100 có chữ số tận cùng là 5
b: \(2^{4k}\) có chữ số tận cùng là 6 với mọi k là số tự nhiên
mà 100=4*25
nên 2^100 có chữ số tận cùng là 6
c: 2023 chia 2 dư 1
mà \(9^{2k+1}\) luôn có chữ số tận cùng là 9
nên \(9^{2023}\) có chữ số tận cùng là 9
d: 2023 chia 4 dư 3
\(7^{4k+3}\left(k\in N\right)\) luôn có chữ số tận cùng là 3
Do đó: \(7^{2023}\) có chữ số tận cùng là 3
Quy luật:
+) các số có c/s tận cg là 0,1,5,6 nâng lên lũy thừa bậc nào (≠0) thì c/s tận cg vẫn là nó.
+) các số có tận cg là 2,4,8 nâng lên lt bậc 4n(n≠0) thì đều có c.s tận cg là 6.
+)các số có c/s tận cg là 3,7,9 nâng lên lt bậc 4n(n≠0) thì đều có c/s tận cg là 1.
+) số có tận cg là 3 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 7
+) số có tận cg là 7 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 3
+) số có tận cg là 2 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 8
+) số có tận cg là 8 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 2
+) số có c/s tận cg là 0,1,4,5,6,9 khi nâng lên lũy thừa bậc 4n+3 thì c/s tận cg là chính nó
Bài 3: áp dụng quy luật bên trên
\(a.5^{100}=\overline{..5}\)
\(b.2^{100}=2^{4.25}=\overline{..6}\)
\(c.9^{2023}=\overline{..9}\)
\(d.7^{2023}=7^{4.505+3}=\overline{...3}\)
Bài 4:
\(A=17^{2008}-11^{2008}-3^{2008}\)
\(=\left(\overline{...7}\right)^{4.502}-\left(\overline{..1}\right)^{2008}-\left(\overline{..3}\right)^{4.502}\)
\(=\overline{..1}-\overline{...1}-\overline{...1}\)
\(=\overline{..9}\)
Bài 5:
\(M=17^{25}+24^4-13^{21}\)
\(=\left(\overline{..7}\right)^{4.6}.\left(\overline{..7}\right)+\left(\overline{..4}\right)^{4.1}-\left(\overline{..3}\right)^{4.5}.\left(\overline{..3}\right)\)
\(\overline{..1}.\overline{..7}+\overline{..6}-\overline{..1}.\overline{..3}\)
\(=\overline{...7}+\overline{..6}-\overline{..3}\)
\(=\overline{...0}\)
\(=>M⋮10\)

giúp e vs ạ e đang cần gấp e xin mng e cần gấp nên mng làm giúp e vs
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)