Tìm cặp số tự nhiên X,Y sao cho : x2 +55=4y2
Tính giá. Trị biểu thức
X13-9x12 +9x11 -9x10+......-9x2 +9x-2
Với x=8
Những câu hỏi liên quan
X13-9x12 +9x11 -9x10+......-9x2 +9x-2
Bạn nên ghi đầy đủ đề (bao gồm yêu cầu cũng như điều kiện về x) để mọi người hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
Tìm cặp số tự nhiên (x y) sao cho x2 +55=4y2
Lời giải:
$x^2+55=4y^2$
$4y^2-x^2=55$
$(2y-x)(2y+x)=55$
Vì $x,y$ là số tự nhiên nên $2y+x, 2y-x$ là số nguyên và $2y+x>0$.
Mà $(2y-x)(2y+x)=55>0$ nên $2y-x>0$
Kết hợp với $2y+x\geq 2y-x$ ta có các TH sau:
TH1: $2y-x=1; 2y+x=55\Rightarrow y=14; x=27$
TH2: $2y-x=5; 2y+x=11\Rightarrow y=4; x=3$
Đúng 1
Bình luận (1)
Tìm cặp số tự nhiên (x,y) sao cho x2 +55=4y2
Lời giải:
$x^2+55=4y^2$
$\Leftrightarrow 55=4y^2-x^2=(2y-x)(2y+x)$
Do $x,y$ là stn nên $2y+x$ là stn.
$\Rightarrow 2y+x>0$. Mà $(2y+x)(2y-x)=55>0$ nên $2y-x>0$.
Vậy $2y+x> 2y-x>0$.
Khi đó ta có các TH sau:
TH1: $2y-x=1, 2y+x=55\Rightarrow y=14; x=27$ (tm)
TH2: $2y-x=5; 2y+x=11\Rightarrow y=4; x=3$ (tm)
Đúng 0
Bình luận (0)
Tìm điều kiện của x để giá trị của biểu thức được xác định:a)
3
x
3
(
x
−
1
)
(
x
2
+
2
)
;
b)
−
4...
Đọc tiếp
Tìm điều kiện của x để giá trị của biểu thức được xác định:
a) 3 x 3 ( x − 1 ) ( x 2 + 2 ) ; b) − 4 x 2 25 − 20 x + 4 x 2 ;
c) x 2 − 9 x 2 − 6 x + 9 2 x ; d) x 2 − 9 x 2 + 6 x + 9 x − 3 .
Cho x, y là hai số thực dương thỏa mãn điều kiện
4
+
9.3
x
2
−
2
y
4
+
9
x
2
−
2
y...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
A. P = 3 + 2 2
B. P = 1 + 9 2
C. P = 9
D. Không tồn tại
Cho x, y là hai số thực dương thỏa mãn điều kiện
4
+
9
.
3
x
2
-
2
y
(
4
+
9
x
2
-
2
y
)
.
7
2...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9 . 3 x 2 - 2 y = ( 4 + 9 x 2 - 2 y ) . 7 2 y - x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
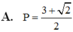
D. Không tồn tại
a, cho x, y là 2 số thoả mãn (2x - y + 7)^{2022} + |x - 1|^{2023} ≤ 0. Tính giá trị của biểu thức: P x^{2023} + (y - 10)^{2023}b, Tìm số tự nhiên x, y biết 25 - y^2 8(x 2023)^2 c, Tìm giá trị nhỏ nhất của biểu thức: P (|x - 3| + 2)^2 + |y + 3| + 2019d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) |y + 1|
Đọc tiếp
a, cho x, y là 2 số thoả mãn (2x - y + 7)\(^{2022}\) + |x - 1|\(^{2023}\) ≤ 0. Tính giá trị của biểu thức: P = x\(^{2023}\) + (y - 10)\(^{2023}\)
b, Tìm số tự nhiên x, y biết 25 - y\(^2\) = 8(x = 2023)\(^2\)
c, Tìm giá trị nhỏ nhất của biểu thức: P = (|x - 3| + 2)\(^2\) + |y + 3| + 2019
d, Tìm cặp số nguyên x, y biết: (2 - x)(x + 1) = |y + 1|
a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)
\(\left|x-1\right|^{2023}>=0\forall x\)
=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)
mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)
nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)
=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)
\(P=x^{2023}+\left(y-10\right)^{2023}\)
\(=1^{2023}+\left(9-10\right)^{2023}\)
=1-1
=0
c: \(\left|x-3\right|>=0\forall x\)
=>\(\left|x-3\right|+2>=2\forall x\)
=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)
mà \(\left|y+3\right|>=0\forall y\)
nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)
=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)
Dấu '=' xảy ra khi x-3=0 và y-3=0
=>x=3 và y=3
Đúng 0
Bình luận (0)
Cho x, y là hai số thực dương thỏa mãn
4
+
9.3
x
2
−
2
y
4
+
9
x
2
−
2
y
.7...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 . Giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x bằng
A. 9
B. 3 + 2 2
C. 1 + 9 2
D. 17
4 tháng 3 2023 lúc 11:39
1. Tìm các số tự nhiên ninleft(1300;2011right) thỏa mãn Psqrt{37126+55n}in N.2. Tìm tất cả cặp số tự nhiên left(x;yright) thỏa mãn xleft(x+y^3right)left(x+yright)^2+7450.3. Tính chính xác giá trị của biểu thức sau dưới dạng phân số tối giản : Adfrac{left(1^4+4right)left(5^4+4right)left(9^4+4right)...left(2005^4+4right)left(2009^4+4right)}{left(3^4+4right)left(7^4+4right)left(11^4+4right)...left(2007^4+4right)left(2011^4+4right)}4. Tìm tất cả các ước nguyên tố của : Sdfrac{2009}{0,left(2009right)...
Đọc tiếp
1. Tìm các số tự nhiên \(n\in\left(1300;2011\right)\) thỏa mãn \(P=\sqrt{37126+55n}\in N\).
2. Tìm tất cả cặp số tự nhiên \(\left(x;y\right)\) thỏa mãn \(x\left(x+y^3\right)=\left(x+y\right)^2+7450\).
3. Tính chính xác giá trị của biểu thức sau dưới dạng phân số tối giản :
\(A=\dfrac{\left(1^4+4\right)\left(5^4+4\right)\left(9^4+4\right)...\left(2005^4+4\right)\left(2009^4+4\right)}{\left(3^4+4\right)\left(7^4+4\right)\left(11^4+4\right)...\left(2007^4+4\right)\left(2011^4+4\right)}\)
4. Tìm tất cả các ước nguyên tố của : \(S=\dfrac{2009}{0,\left(2009\right)}+\dfrac{2009}{0,0\left(2009\right)}+\dfrac{2009}{0,00\left(2009\right)}\).