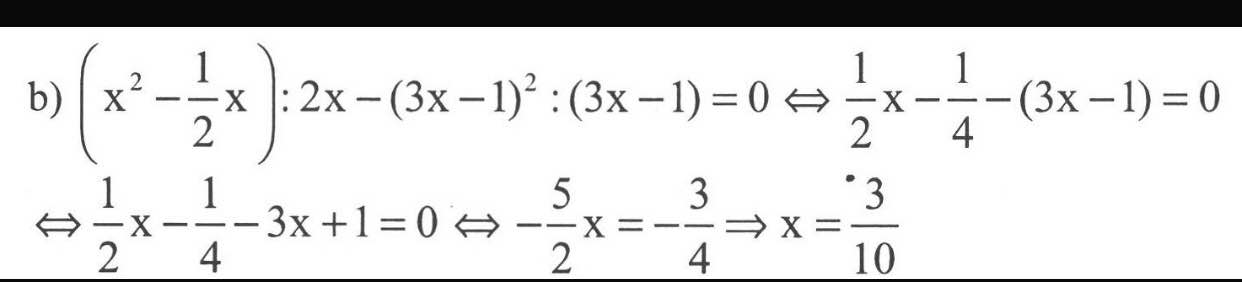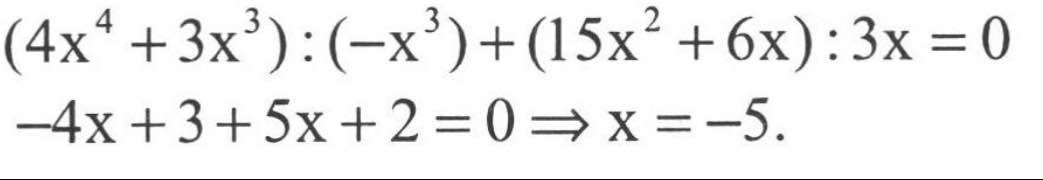\(\dfrac{3x^2+4x-1}{x+1}\)

\(=\dfrac{3x^2+3x+x+1-2}{x+1}\)

\(=3x+1+\dfrac{-2}{x+1}\)

1: Sửa đề: 3x-5

\(=\dfrac{-x^2\left(3x-5\right)-3\left(3x-5\right)}{3x-5}=-x^2-3\)

2: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)

=5x^2+14x^2+12x+8

3: \(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}=5x^2+4x+4\)

4: \(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}=x^2+1-2x\)

5: \(=\dfrac{x^2\left(5-3x\right)+3\left(5-3x\right)}{5-3x}=x^2+3\)

c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)

\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)

\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)

\(=5x^3+14x^2+12x+8\)

d) Ta có: \(\dfrac{5x^3+14x^2+12x+8}{x+2}\)

\(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}\)

\(=\dfrac{5x^2\left(x+2\right)+4x\left(x+2\right)+4\left(x+2\right)}{x+2}\)

\(=5x^2+4x+4\)

c) Ta có: \(\dfrac{5x^4+9x^3-2x^2-4x-8}{x-1}\)

\(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)

\(=\dfrac{5x^3\left(x-1\right)+14x^2\left(x-1\right)+12x\left(x-1\right)+8\left(x-1\right)}{x-1}\)

\(=5x^3+14x^2+12x+8\)

a) Đa thức thương  x 2  + 3x – 1 và đa rhức dư -4.

Kiểm tra bằng cách thực hiện (3x + 1)( x 2  + 3x – 1) + (-4),

b) Đa thức thương x + 2 và đa thức dư –x + 5.

Đây nhé! Tích giúp mình nha

Ta có: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)

\(\Leftrightarrow-4x-3+5x+2=0\)

\(\Leftrightarrow x-1=0\)

hay x=1

\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)

Thay \(x=1\)

\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)

\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)

Thay \(x=1\)

\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)

Thay \(x=3\)

\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)

Vậy \(a=-12\)