a)

Theo tính chất kề bù có:

\(\widehat{xOy}+\widehat{xOy'}=180^o\\ \Rightarrow\widehat{xOy'}=180^o-130^o=50^o\)

b)

Vì Ot là tia phân giác của \(\widehat{xOy}\) nên:

\(\widehat{tOx}=\dfrac{\widehat{xOy}}{2}=\dfrac{130^o}{2}=65^o\)

Vì Ot' là tia phân giác của \(\widehat{xOy'}\) nên:

\(\widehat{xOt'}=\dfrac{\widehat{xOy'}}{2}=\dfrac{50^o}{2}=25^o\)

Số đo góc \(\widehat{tOt'}\) là:

\(\widehat{tOt'}=\widehat{tOx}+\widehat{xOt'}=65^o+25^o=90^o\)

a) 50^o

b) 90^o

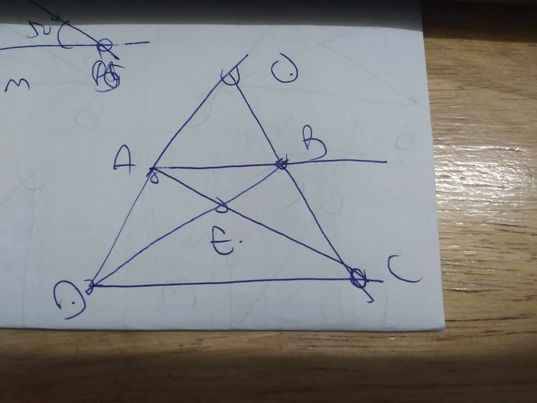
a: OA<OB

=>A nằm giữa O và B

=>OA+AB=OB

=>AB=2cm

b: Vì OA<OC

nên A nằm giữa O và C

mà OA=1/2OC

nên A là trung điểm của OC

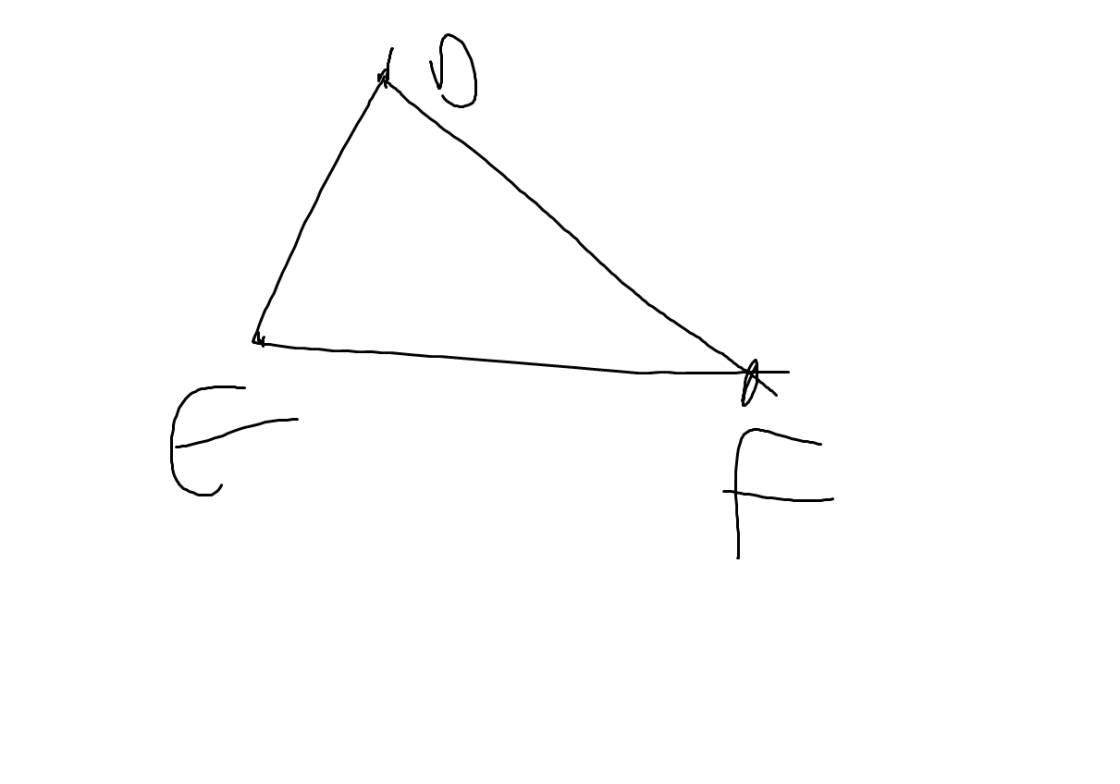
Xét ΔDEF có DE<DF<EF

mà \(\widehat{F};\widehat{E};\widehat{D}\) lần lượt là góc đối diện của các cạnh DE,DF,EF

nên \(\widehat{F}< \widehat{E}< \widehat{D}\)

Em chụp hình bài đó lại nhé!

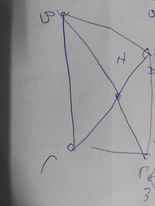
a: Xét ΔIAE và ΔICB có

IA=IC

\(\widehat{AIE}=\widehat{CIB}\)

IE=IB

Do đó: ΔAIE=ΔCIB

=>AE=CB

b: ΔAIE=ΔCIB

=>\(\widehat{IAE}=\widehat{ICB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AE//BC

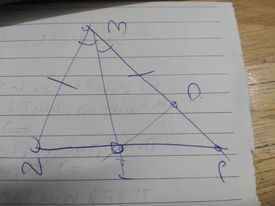
a: Xét ΔMNI và ΔMDI có

MN=MD

\(\widehat{NMI}=\widehat{DMI}\)

MI chung

Do đó: ΔMNI=ΔMDI

b: Ta có: ΔMNI=ΔMDI

=>IN=ID

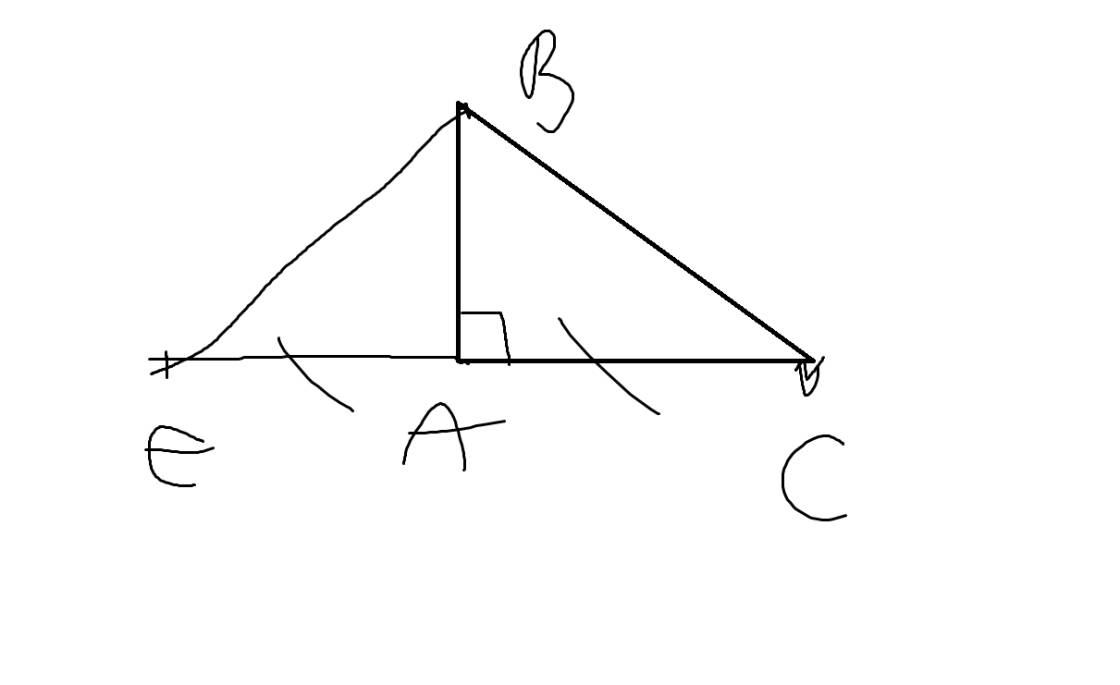
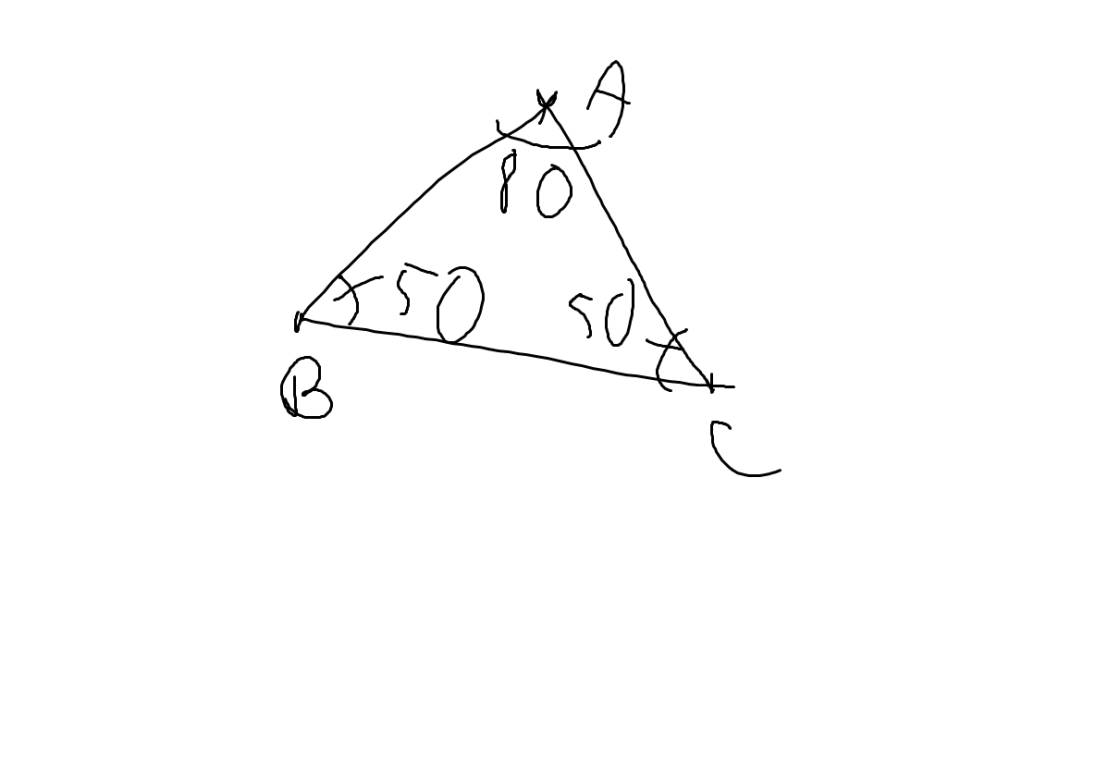
a) Xét \(\Delta ABC\) có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\) (định lí tổng các góc trong tam giác)

\(\Rightarrow \widehat{B}=180^\circ-\widehat{A}-\widehat{C}\)

\(\Rightarrow\widehat{B}=180^\circ-80^\circ-50^\circ=50^\circ\) (vì \(\widehat{A}=80^\circ;\widehat{C}=50^\circ\))

Khi đó: \(\widehat{A}>\widehat{B}=\widehat{C}\) (vì \(80^{\circ}>50^{\circ}=50^{\circ}\))

\(\Rightarrow BC>AB=AC\) (theo đli quan hệ giữa góc và cạnh đối diện trong tam giác)

\(\Rightarrow BC\) là cạnh lớn nhất của \(\Delta ABC\)

b) Xét \(\Delta ABC\) có: \(AB=AC\) (cmt)

\(\Rightarrow\Delta ABC\) cân tại \(A\)

a: Xét ΔABC có \(\widehat{A}+\widehat{C}+\widehat{B}=180^0\)

=>\(\widehat{B}=180^0-80^0-50^0=50^0\)

Xét ΔABC có \(\widehat{A}>\widehat{B}=\widehat{C}\)

mà BC,AC,AB lần lượt là các cạnh đối diện của các góc \(\widehat{A};\widehat{B};\widehat{C}\)

nên BC>AC=AB

=>BC là cạnh lớn nhất trong ΔABC

b: Xét ΔABC có \(\widehat{B}=\widehat{C}\)

nên ΔABC cân tại A