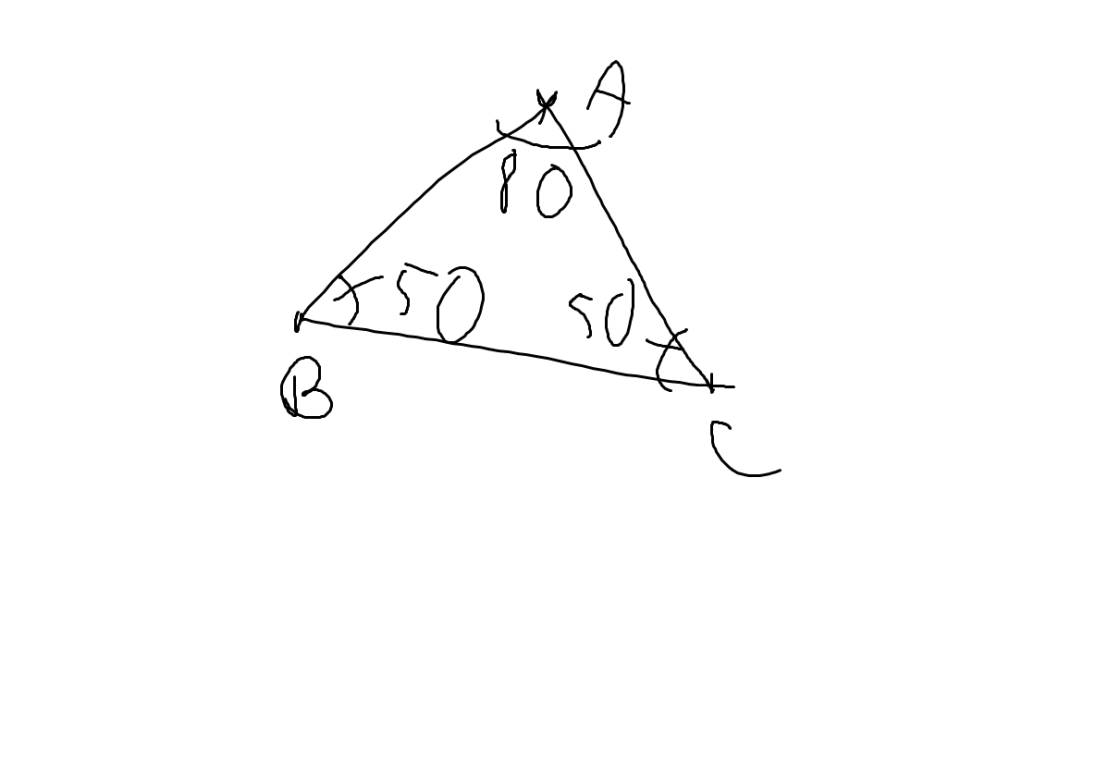
a) Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\) (định lí tổng các góc trong tam giác)
\(\Rightarrow \widehat{B}=180^\circ-\widehat{A}-\widehat{C}\)
\(\Rightarrow\widehat{B}=180^\circ-80^\circ-50^\circ=50^\circ\) (vì \(\widehat{A}=80^\circ;\widehat{C}=50^\circ\))
Khi đó: \(\widehat{A}>\widehat{B}=\widehat{C}\) (vì \(80^{\circ}>50^{\circ}=50^{\circ}\))
\(\Rightarrow BC>AB=AC\) (theo đli quan hệ giữa góc và cạnh đối diện trong tam giác)
\(\Rightarrow BC\) là cạnh lớn nhất của \(\Delta ABC\)
b) Xét \(\Delta ABC\) có: \(AB=AC\) (cmt)
\(\Rightarrow\Delta ABC\) cân tại \(A\)
a: Xét ΔABC có \(\widehat{A}+\widehat{C}+\widehat{B}=180^0\)
=>\(\widehat{B}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}>\widehat{B}=\widehat{C}\)
mà BC,AC,AB lần lượt là các cạnh đối diện của các góc \(\widehat{A};\widehat{B};\widehat{C}\)
nên BC>AC=AB
=>BC là cạnh lớn nhất trong ΔABC
b: Xét ΔABC có \(\widehat{B}=\widehat{C}\)
nên ΔABC cân tại A