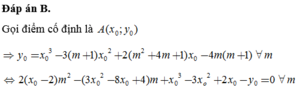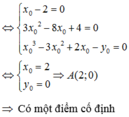quy đồng lên cộng vào rút gọn

1: \(\Leftrightarrow x\left(m+1-1\right)-2=0\)

=>mx-2=0

Để phương trình vô nghiệm thì m=0

2: \(\Leftrightarrow x\left(m^2+2m+1-4m-9\right)=m+2\)

\(\Leftrightarrow x\left(m^2-2m-8\right)=m+2\)

Để phương trình vô nghiệm thì m-4=0

hay m=4

3: \(\Leftrightarrow m^2x-m^2=4x-2m-8\)

\(\Leftrightarrow x\left(m^2-4\right)=m^2-2m-8=\left(m-4\right)\left(m+2\right)\)

để pt vô nghiệm thì m-2=0

hay m=2

a) \(\frac{1}{m+1}+\frac{1}{\left(m+1\right)\left(2m+1\right)}\)

\(=\frac{2m+1}{\left(m+1\right)\left(2m+1\right)}+\frac{1}{\left(m+1\right)\left(2m+1\right)}\)

\(=\frac{2m+2}{\left(m+1\right)\left(2m+1\right)}\)

\(=\frac{2\left(m+1\right)}{\left(m+1\right)\left(2m+1\right)}\)

\(=\frac{2}{2m+1}=\frac{4}{4m+2}\left(đpcm\right)\)

b) \(\frac{1}{m+2}+\frac{1}{\left(m+1\right)\left(m+2\right)}+\frac{1}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{m+1}{\left(m+1\right)\left(m+2\right)}+\frac{1}{\left(m+1\right)\left(m+2\right)}+\frac{1}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{m+2}{\left(m+1\right)\left(m+2\right)}+\frac{1}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{1}{m+1}+\frac{1}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{4m+3}{\left(m+1\right)\left(4m+3\right)}+\frac{1}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{4m+4}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{4\left(m+1\right)}{\left(m+1\right)\left(4m+3\right)}\)

\(=\frac{4}{4m+3}\left(đpcm\right)\)

Loại bài này trước hết phải phân tích để mò coi pt có nghiệm cố định nào không:

\(x^3-3\left(m+1\right)x^2+2\left(m^2+4m+1\right)x-4m\left(m+1\right)=0\)

\(\Leftrightarrow2\left(x-2\right)m^2+\left(-3x^2+8x-4\right)m+\left(x^3-3x^2+2x\right)=0\)

\(\Rightarrow\left\{{}\begin{matrix}2\left(x-2\right)=0\\-3x^2+8x-4=0\\x^3-3x^2+2x=0\end{matrix}\right.\)

Cả 3 pt trên đều có nghiệm \(x=2\), vậy pt đã cho luôn có nghiệm cố định \(x=2\) với mọi m, sử dụng lược đồ Hoocne để hạ bậc ta đưa được pt về:

\(x^3-3\left(m+1\right)x^2+2\left(m^2+4m+1\right)x-4m\left(m+1\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-\left(3m+1\right)x+2m^2+2m\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-\left(3m+1\right)x+2m^2+2m=0\left(1\right)\end{matrix}\right.\)

Để pt đã cho có 3 nghiệm pb đều lớn hơn 1 \(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb lớn hơn 1 và khác 2

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\f\left(1\right)>0\\\frac{x_1+x_2}{2}>1\\f\left(2\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(3m+1\right)^2-4\left(2m^2+2m\right)>0\\1-\left(3m+1\right)+2m^2+2m>0\\3m+1>2\\4-2\left(3m+1\right)+2m^2+2\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2>0\\2m^2-m>0\\m>\frac{1}{3}\\2m^2-4m+2\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>\frac{1}{2}\\m\ne1\end{matrix}\right.\)

+ Phương trình hoành độ giao điểm của đồ thị C  và trục Ox:

x³- 3( m+ 1) x²+ 2( m ²+ 4m+1 )= 0

hay ( x- 2) ( x²-( 3m+ 1) x+ 2m²+ 2m) =0

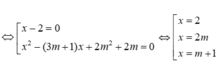
Yêu cầu bài toán

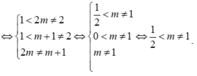
Vậy ½< m và m≠ 1.

Chọn A.

Đáp án B.

Gọi điểm cố định là  A ( x 0 ; y 0 )

⇒ y 0 = x 0 3 − 3 ( m + 1 ) x 0 2 + 2 ( m 2 + 4 m + 1 ) x 0 − 4 m ( m + 1 )   ∀ m  

⇔ 2 ( x 0 − 2 ) m 2 − ( 3 x 0 2 − 8 x 0 + 4 ) m + x 0 3 − 3 x o 2 + 2 x 0 − y 0 = 0   ∀ m  

⇔ x 0 − 2 = 0 3 x 0 2 − 8 x 0 + 4 = 0 x 0 3 − 3 x 0 2 + 2 x 0 − y 0 = 0 ⇔ x 0 = 2 y 0 = 0 ⇒ A ( 2 ; 0 )  

=>Có một điểm cố định