Số học sinh trung bình chiếm:

\(100\%-36\%-48\%=16\%\)

Số học sinh lớp 5A là:

\(8:16\%=50\left(bạn\right)\)

Số học sinh giỏi là:

\(50\cdot36\%=18\left(bạn\right)\)

Số học sinh khá là:

\(50\cdot48\%=24\left(bạn\right)\)

Bài 3:

Nếu đáy lớn được tăng thêm 5 cm thì diện tích sẽ tăng một phần bằng 5 x chiều cao : 2

Vậy chiều cao của hình thang là:
$20\times 2:5=2$ (m) 

Diện tích hình thang ban đầu là:

$50\times 2:2=50$ (m²)

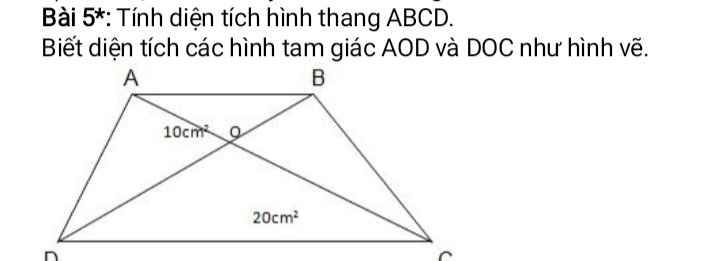
\(\dfrac{S_{AOD}}{S_{DOC}}=\dfrac{10}{20}=\dfrac{1}{2}\)

=>\(AO=\dfrac{1}{2}CO\)

Vì ABCD là hình thang có hai đáy là AB và CD

và AC cắt BD tại O

nên \(S_{AOD}=S_{BOC}\)

=>\(S_{BOC}=10\left(cm^2\right)\)

\(AO=\dfrac{1}{2}OC\)

=>\(S_{AOB}=\dfrac{1}{2}\cdot S_{BOC}=5\left(cm^2\right)\)

\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)

\(=5+10+20+10=45\left(cm^2\right)\)

\(\dfrac{13}{2}\) : 4\(\dfrac{2}{3}\): 2

= \(\dfrac{13}{2}\): \(\dfrac{14}{3}\):2

= \(\dfrac{13}{2}\) \(\times\) \(\dfrac{3}{14}\):2

=  \(\dfrac{39}{28}\) : 2

= \(\dfrac{39}{28}\) \(\times\) \(\dfrac{1}{2}\)

= \(\dfrac{39}{56}\)

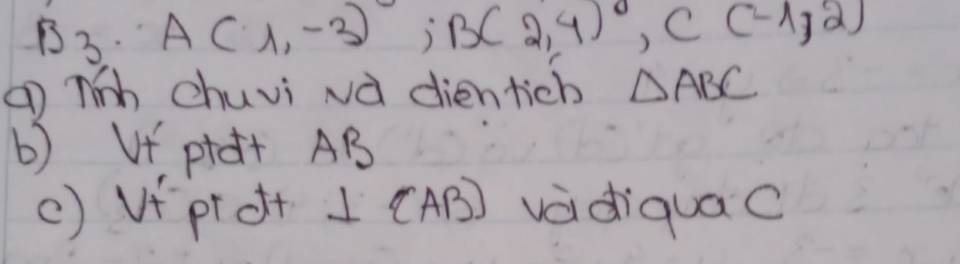
a: A(1;-3); B(2;4); C(-1;2)

\(AB=\sqrt{\left(2-1\right)^2+\left(4+3\right)^2}=5\sqrt{2}\)

\(BC=\sqrt{\left(-1-2\right)^2+\left(2-4\right)^2}=\sqrt{13}\)

\(AC=\sqrt{\left(-1-1\right)^2+\left(2+3\right)^2}=\sqrt{29}\)

Chu vi tam giác ABC là:

\(C_{ABC}=AB+BC+AC=5\sqrt{2}+\sqrt{13}+\sqrt{29}\)

Xét ΔABC có

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)

\(=\dfrac{50+29-13}{2\cdot5\sqrt{2}\cdot\sqrt{29}}=\dfrac{33}{5\sqrt{58}}\)

\(sin^2A+cos^2A=1\)

=>\(sin^2A=1-\left(\dfrac{33}{5\sqrt{58}}\right)^2=\dfrac{361}{1450}\)

=>\(sinA=\sqrt{\dfrac{361}{1450}}\)

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{\dfrac{361}{1450}\cdot50\cdot29}=\dfrac{19}{2}\)

b: Gọi (d): y=ax+b là phương trình đường thẳng AB

(d) đi qua A(1;-3) và B(2;4) nên ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=-3\\2a+b=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-a=-7\\a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-3-a=-3-7=-10\end{matrix}\right.\)

Vậy: (d): y=7x-10

c: Gọi (d1):y=ax+b là phương trình đường thẳng cần tìm

Vì (d1) vuông góc AB nên \(a\cdot7=-1\)

=>\(a=-\dfrac{1}{7}\)

=>(d1): \(y=-\dfrac{1}{7}x+b\)

Thay x=-1 và y=2 vào (d1), ta được:

\(b+\dfrac{1}{7}=2\)

=>\(b=2-\dfrac{1}{7}=\dfrac{13}{7}\)

Vậy: (d1): \(y=-\dfrac{1}{7}x+\dfrac{13}{7}\)

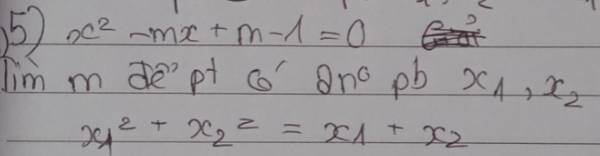
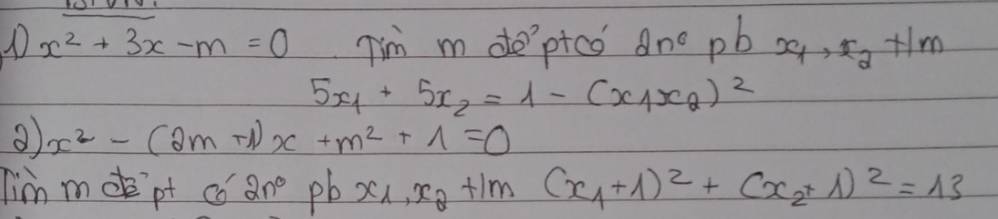
5.

\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)

Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)

Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)

\(x_1^2+x_2^2=x_1+x_2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)

\(\Leftrightarrow m^2-2\left(m-1\right)=m\)

\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)

1.

\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)

\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)

\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)

\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)

\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)

2.

\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)

\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)

\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)

\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)

\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)

\(\Leftrightarrow2m^2+8m-10=0\)

\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)