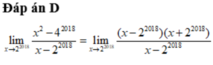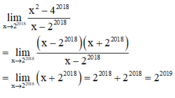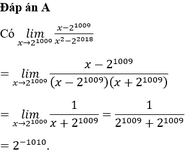22018-22017

Những câu hỏi liên quan
B = 22018 - 22017 - 22016 - 22015 - 22014
\(B=2^{2018}-2^{2017}-2^{2016}-2^{2015}-2^{2014}\)
\(=>2B=2^{2019}-2^{2018}-2^{2017}-2^{2016}-2^{2015}\)
\(=>2B+B=2^{2019}-2^{2014}\)
\(=>B=\dfrac{2^{2019}-2^{2014}}{3}\)
Đúng 3
Bình luận (0)
21+ 22 + 23+... +22017
`@` Đặt `A=2^1+2^2+2^3+...+2^2017`
`=>2A=2(2^1+2^2+2^3+...+2^2017)`
`=>2A=2^2+2^3+...+2^2018`
`=>2A-A=(2^2+2^3+...+2^2018)-(2^1+2^2+...+2^2017)`
`=>A=2^2018-2`
Đúng 0
Bình luận (0)
A = 2 + 22 + 23 + … + 22017
Sửa đề: A=2+2^2+2^3+...+2^2017
=>2*A=2^2+2^3+2^4+...+2^2018
=>2A-A=2^2018-2
=>A=2^2018-2
Đúng 0
Bình luận (0)
lim
x
→
2
2018
x
2
-
4
2018
x
-
2
2018
A.
2
2019
B.
2...
Đọc tiếp
lim x → 2 2018 x 2 - 4 2018 x - 2 2018
A. 2 2019
B. 2 2018
C. 2
D. + ∞
lim
x
→
2018
x
2
-
4
2018
x
-
2
2018
bằng: A.
+
∞
B. 2 C.
2
2018
D.
2
2019
Đọc tiếp
lim x → 2018 x 2 - 4 2018 x - 2 2018 bằng:
A. + ∞
B. 2
C. 2 2018
D. 2 2019
lim
x
→
2
2018
x
2
−
4
2018
x
−
2
2018
bằng A.
2
2019
B.
+
∞
C. 2 D. ...
Đọc tiếp
lim x → 2 2018 x 2 − 4 2018 x − 2 2018 bằng
A. 2 2019
B. + ∞
C. 2
D. 2 2018
Tính
l
i
m
x
→
2
1009
x
-
2
1009
x
2
-
2
2018
A.
2
-
1010
B. ...
Đọc tiếp
Tính l i m x → 2 1009 x - 2 1009 x 2 - 2 2018
A. 2 - 1010
B. 2 1009
C. 2 1010
D. 2 - 1009
lim
x
→
2018
x
2
-
4
2018
x
-
2
2018
bằng A.
+
∞
B.2 C.
2
2018
D.
2...
Đọc tiếp
lim x → 2018 x 2 - 4 2018 x - 2 2018 bằng
A. + ∞
B.2
C. 2 2018
D. 2 2019
lim
x
→
2018
x
2
−
4
2018
x
−
2
2018
bằng: A.
+
∞
.
B. 2 C. ...
Đọc tiếp
lim x → 2018 x 2 − 4 2018 x − 2 2018 bằng:
A. + ∞ .
B. 2
C. 2 2018 .
D. 2 2019 .
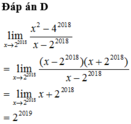
Đáp án D
lim x → 2 2018 x 2 − 4 2018 x − 2 2018 = lim x → 2 2018 ( x − 2 2018 ) ( x + 2 2018 ) x − 2 2018 = lim x → 2 2018 x + 2 2018 = 2 2019
Đúng 0
Bình luận (0)