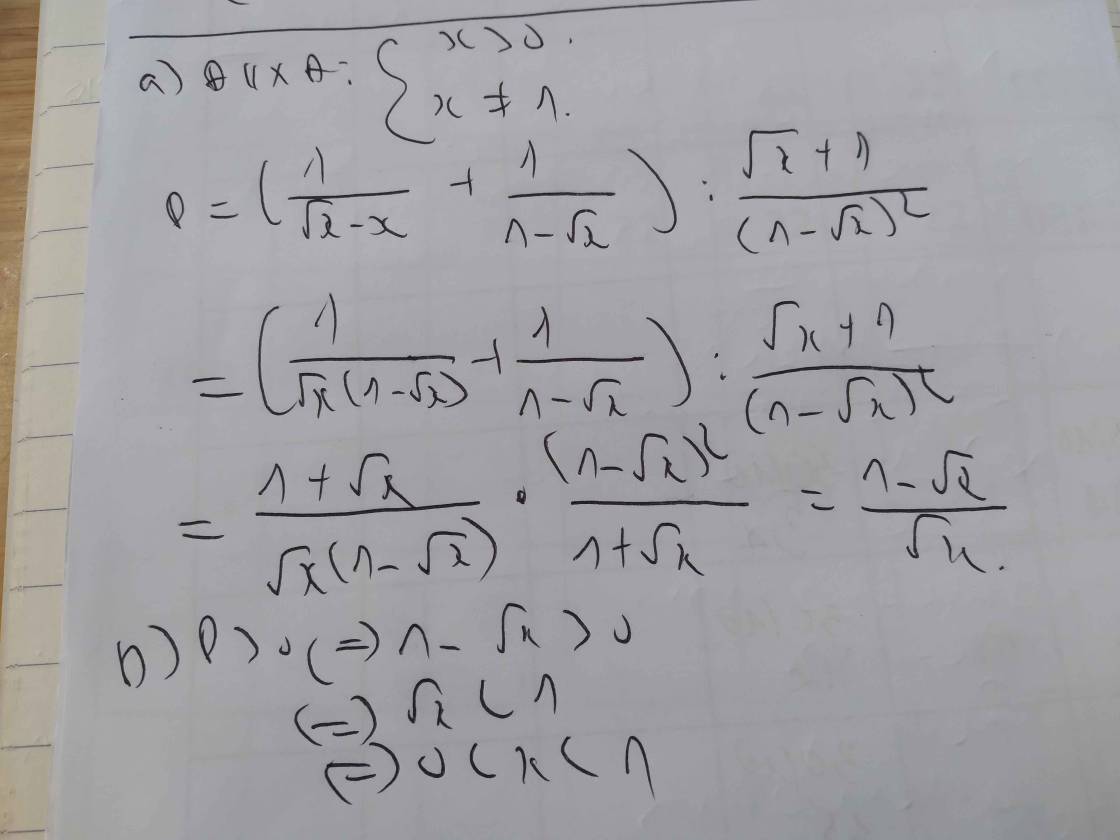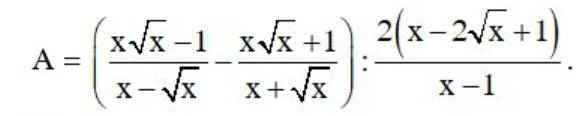
a,rút gọn
b,tìm x để A<0

Những câu hỏi liên quan
a,rút gọn
b,tìm x để A<1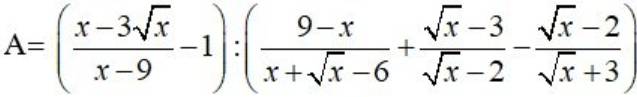
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
\(A=\left(\dfrac{x-3\sqrt{x}}{x-9}-1\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\dfrac{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-1\right):\left(\dfrac{3-x+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)
\(=\dfrac{\sqrt{x}-\sqrt{x}-3}{\sqrt{x}+3}:\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\)
\(=\dfrac{-3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{3}{\sqrt{x}-2}\)
b: A<1
=>A-1<0
=>\(\dfrac{3-\sqrt{x}+2}{\sqrt{x}-2}< 0\)
=>\(\dfrac{\sqrt{x}-5}{\sqrt{x}-2}>0\)
TH1: \(\left\{{}\begin{matrix}\sqrt{x}-5>0\\\sqrt{x}-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>5\\\sqrt{x}>2\end{matrix}\right.\Leftrightarrow\sqrt{x}>5\)
=>x>25
TH2: \(\left\{{}\begin{matrix}\sqrt{x}-5< 0\\\sqrt{x}-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}< 2\\\sqrt{x}< 5\end{matrix}\right.\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
Đúng 2
Bình luận (0)
cho A = \(\left(\dfrac{3}{x-1}+\dfrac{1}{\sqrt{x}+1}\right):\dfrac{1}{\sqrt{x}+1}\) với x ≥ 0 và x ≠ 1
a, Rút gọn
b, tìm x để A = \(\dfrac{5}{4}\)
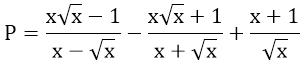
a) Rút gọn
b) Tìm x sao cho P = 9/2
\(P=\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}\)
\(\Rightarrow P=\dfrac{x\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{x\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{\left(x+1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\left(x\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(x\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\left(x+1\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{x-\sqrt{x}+x\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}-x\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\left(x+1\right)\left(x-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{x-\sqrt{x}+x\sqrt{x}-1-\left(x+\sqrt{x}-x\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x^2-1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{x-\sqrt{x}+x\sqrt{x}-1-x-\sqrt{x}+x\sqrt{x}+1+x^2-1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{x^2-2\sqrt{x}+2x\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
Đúng 0
Bình luận (0)
cho biểu thức
P=\(\left(\dfrac{1}{\sqrt{x}-x}+\dfrac{1}{1-\sqrt{x}}\right)\):\(\dfrac{\sqrt{x}+1}{\left(1-\sqrt{x}\right)^2}\)
a) tìm đk và rút gọn
b) Tìm x để P>0
A=\(\dfrac{2x+9\sqrt{x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}-\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
a)rút gọn
b)tìm giá trị nguyên của x để A CÓ GIÁ TRỊ NGUYÊN
M=\(\left(\dfrac{x}{x-2}-\dfrac{x+1}{x+2}-\dfrac{2x+7}{x^{2^{ }}-4}\right):\left(\dfrac{3-x}{x-2}+1\right)\)
a,rút gọn
b,tìm x để M <1
a. ĐK: \(x\ne\pm2\)
\(M=\left[\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x+7}{\left(x-2\right)\left(x+2\right)}\right]:\dfrac{3-x+x-2}{x-2}\)
\(=\dfrac{x^2+2x-\left(x^2-2x+x-2\right)-2x-7}{\left(x-2\right)\left(x+2\right)}.\left(x-2\right)\)
\(=\dfrac{x-5}{x+2}\)
b. \(\dfrac{x-5}{x+2}< 1\Leftrightarrow\dfrac{x-5}{x+2}-1< 0\)
\(\Leftrightarrow\dfrac{-7}{x+2}< 0\Leftrightarrow x+2>0\)
\(\Leftrightarrow x>-2\)
Vậy \(x>-2,x\ne2\)
Đúng 2
Bình luận (0)
Cho biểu thức A=\(\dfrac{\sqrt{x}+1}{x+4\sqrt{x}+4}:\left(\dfrac{x}{x+2\sqrt{x}}+\dfrac{x}{\sqrt{x}+2}\right)\)( x ≥ 0)
a) Rút gọn
b) Tìm x để A ≥ \(\dfrac{1}{3\sqrt{x}}\)
(mink đag cần gấp)
a, A= \(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\left(\sqrt{x}\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)
A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}}{\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)
A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}+x}{\left(\sqrt{x}+2\right)}\right)\)
A=\(\frac{1}{x+2\sqrt{x}}\)
b, A >= \(\frac{1}{3\sqrt{x}}\)
=> \(\frac{1}{x+2\sqrt{x}}\) >= \(\frac{1}{3\sqrt{x}}\)
=> x <= -1 , x >= 4 (x khác 0)
Cho biểu thức A=\(\dfrac{\sqrt{x}+1}{x+4\sqrt{x}+4}:\left(\dfrac{x}{x+2\sqrt{x}}+\dfrac{x}{\sqrt{x}+2}\right)\)( x ≥ 0)
a) Rút gọn
b) Tìm x để A ≥ \(\dfrac{1}{3\sqrt{x}}\)
(mink đag cần gấp)
B1: Aleft(dfrac{2-3x}{x^2+2x-3}-dfrac{x+3}{1-x}-dfrac{x+1}{x+3}right):dfrac{3x+12}{x^3-1}a) Rút gọnb) Tìm x thuộc Z để A nguyênc) Tính A với x-2; x-3d) Tìm x dể A1B2: Phân tích thành nhân tửa) x2-2xy-4+y2b) x2-4x+3c) 9x2(x-y)-x+yB3: Rút gọna) (x-2)3-(x+2)3-(x-1)(x2+x+1)b) (5x+3y)(5x-3y)+(4x-3y)2B4: P(x)x4+x3+mx2-3x+5a) Khi m4, thực hiện phép chia P(x) cho x2-x+1b) Tìm m để P(x)⋮(x-1)
Đọc tiếp
B1: A=\(\left(\dfrac{2-3x}{x^2+2x-3}-\dfrac{x+3}{1-x}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{x^3-1}\)
a) Rút gọn
b) Tìm x thuộc Z để A nguyên
c) Tính A với x=-2; x=-3
d) Tìm x dể A=1
B2: Phân tích thành nhân tử
a) x2-2xy-4+y2
b) x2-4x+3
c) 9x2(x-y)-x+y
B3: Rút gọn
a) (x-2)3-(x+2)3-(x-1)(x2+x+1)
b) (5x+3y)(5x-3y)+(4x-3y)2
B4: P(x)=x4+x3+mx2-3x+5
a) Khi m=4, thực hiện phép chia P(x) cho x2-x+1
b) Tìm m để P(x)⋮(x-1)