giúp mình bài 3 ạ

Những câu hỏi liên quan
các bn giúp mình bài 1, bài 2 trang 29 hình ở trên ạcác bn giúp mình bài 3, hình ở trên ạ các bn giúp mình bài 4, trang 30 hình ở trên ạ mong mn giúp đỡ mình ạ !!!
Đọc tiếp
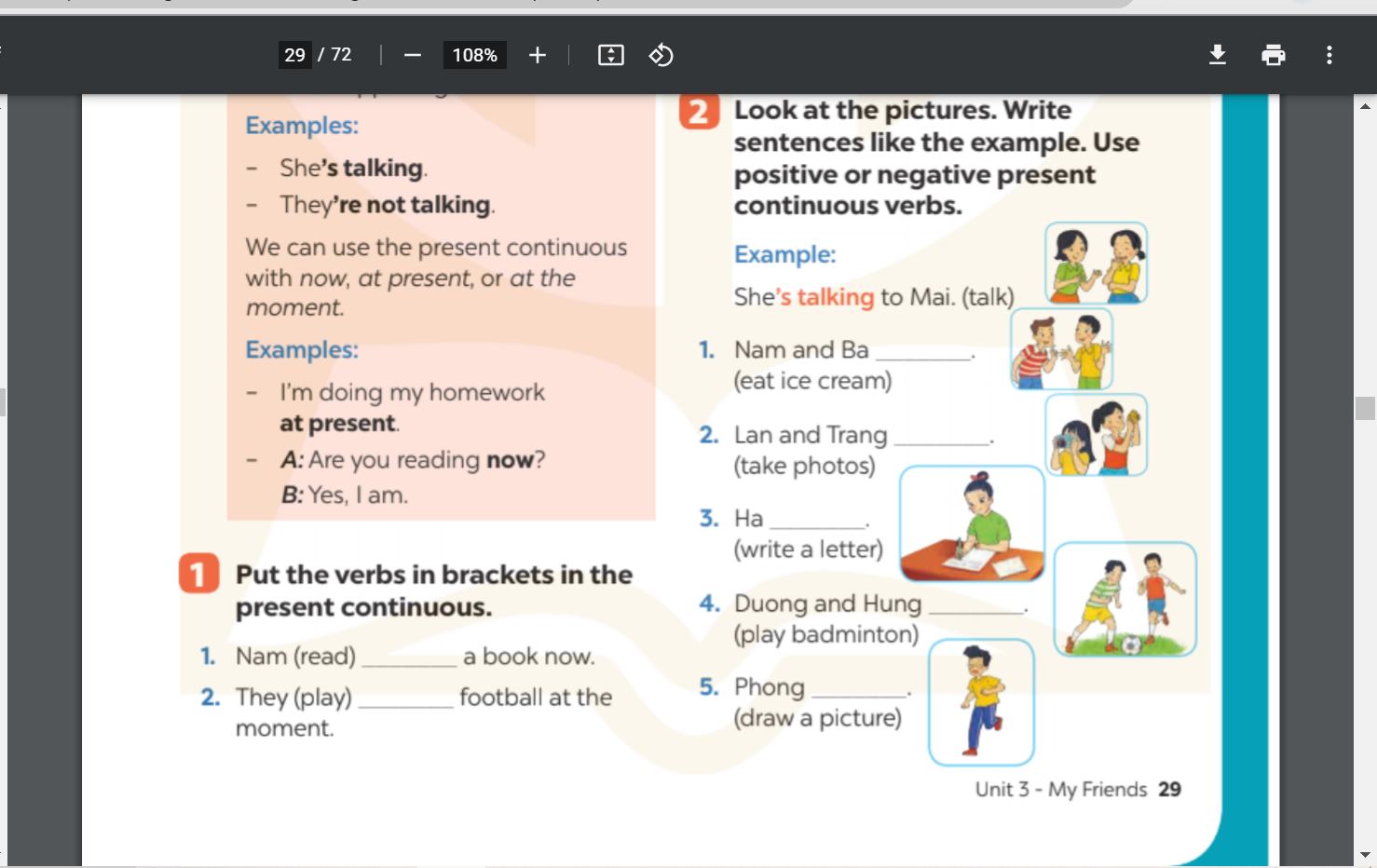
các bn giúp mình bài 1, bài 2 trang 29 hình ở trên ạ
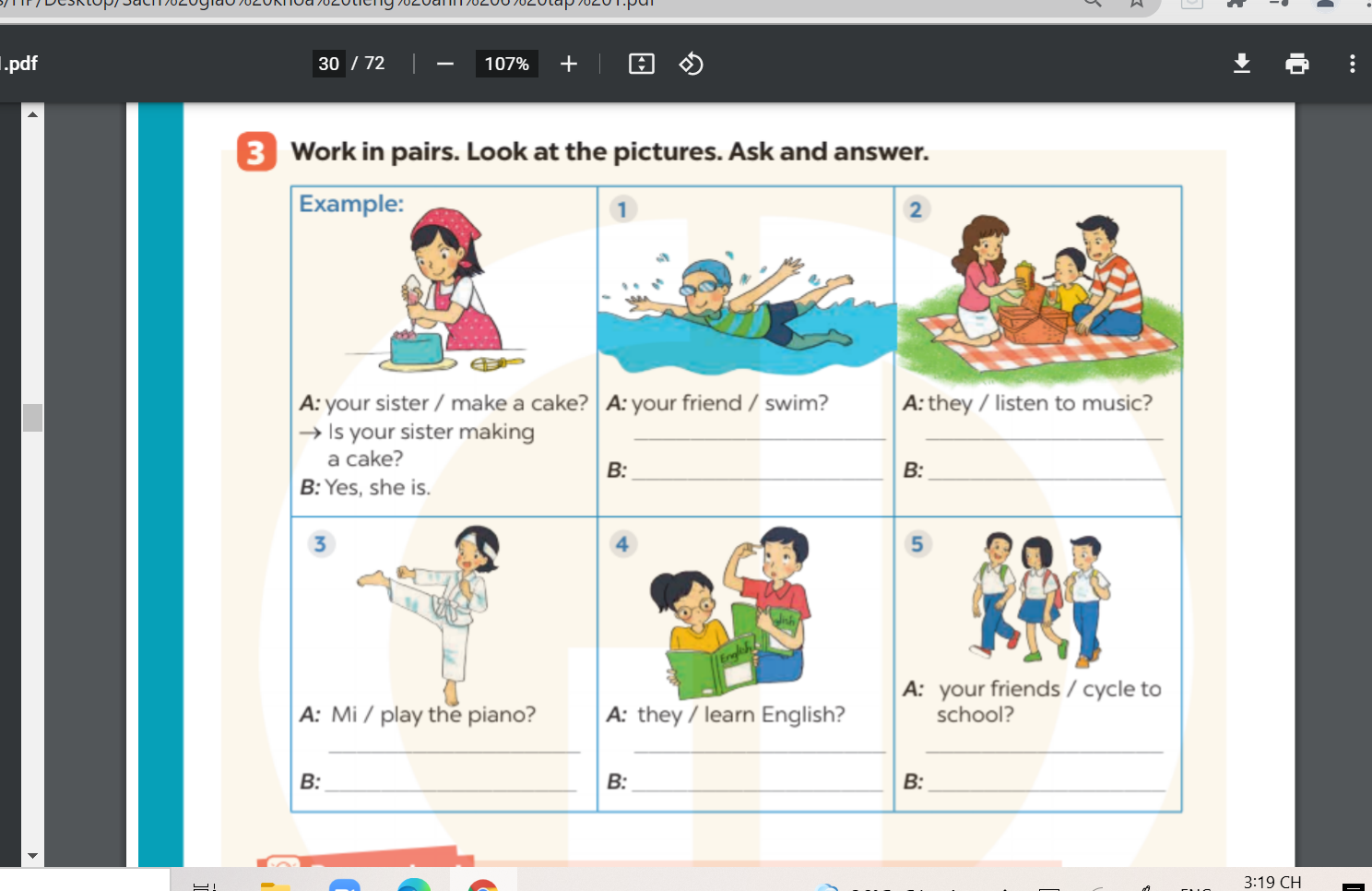
các bn giúp mình bài 3, hình ở trên ạ
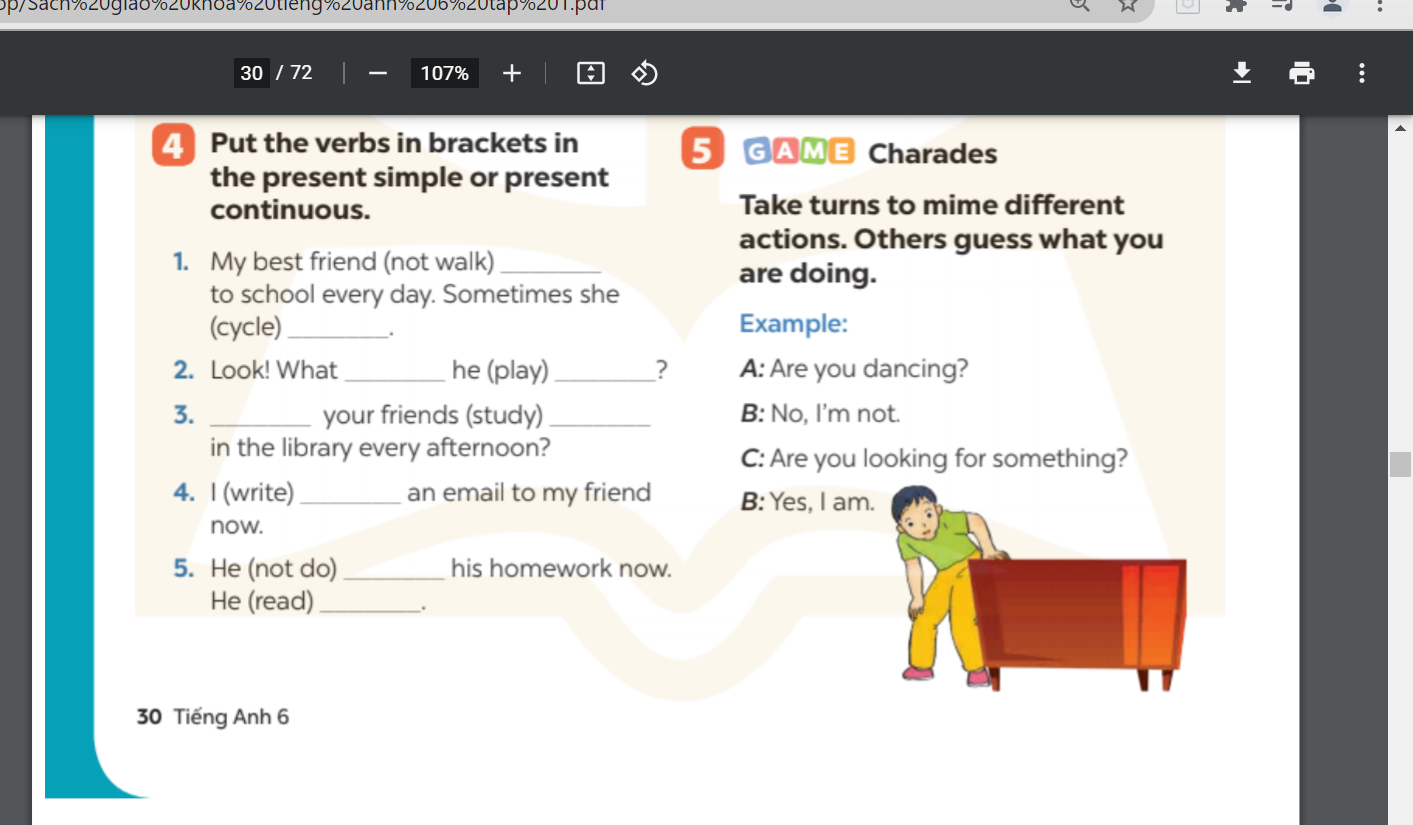 các bn giúp mình bài 4, trang 30 hình ở trên ạ
các bn giúp mình bài 4, trang 30 hình ở trên ạ
mong mn giúp đỡ mình ạ !!! ![]()
1) are eatting ....
2)are talking...
3)Ha is writing...
4)are playing...
5)is drawing...
4)
Đúng 2
Bình luận (0)
1) Are your friend swimming
yes, it is
2)Are they listen to music
yes, they are
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
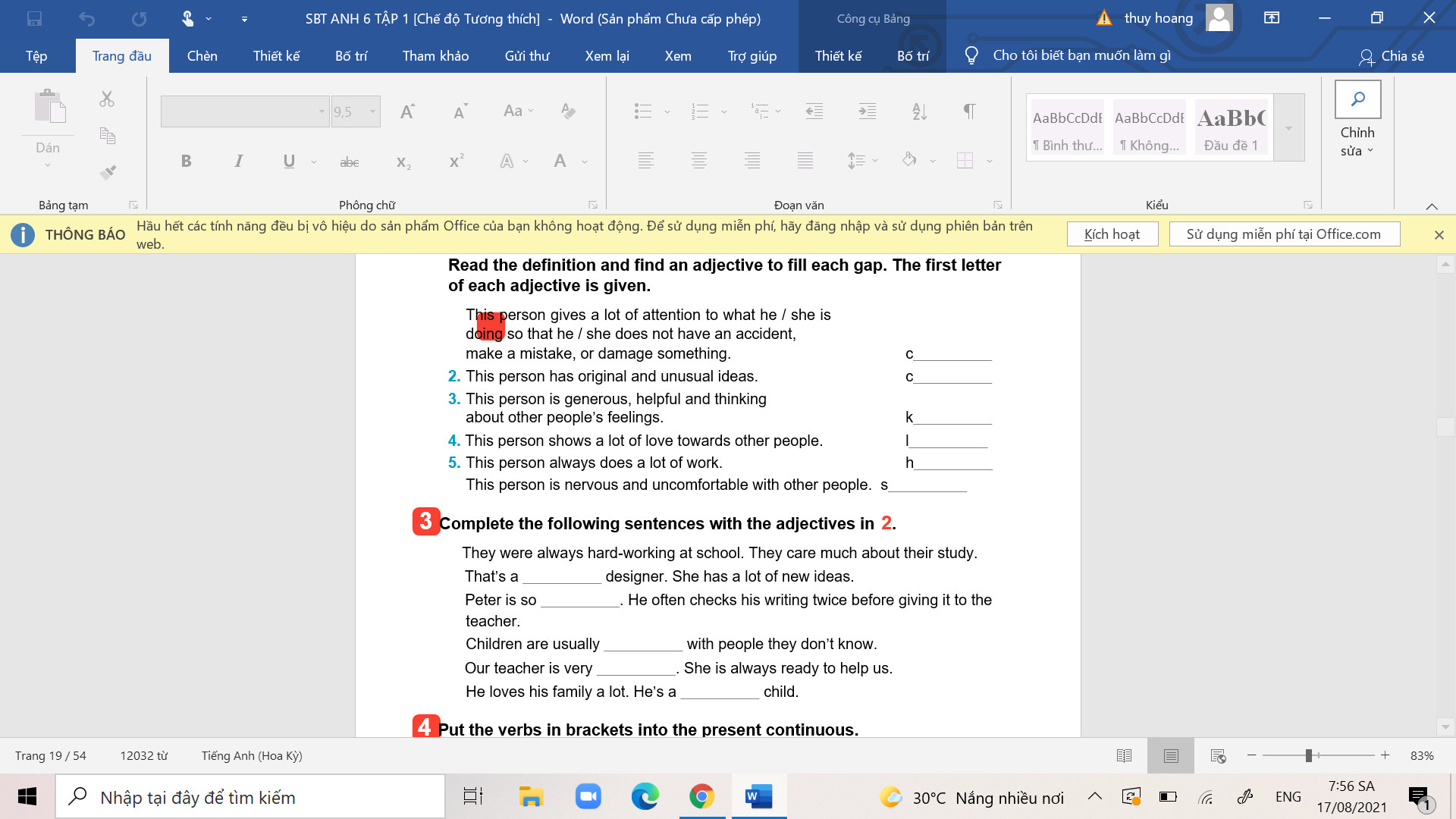 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.
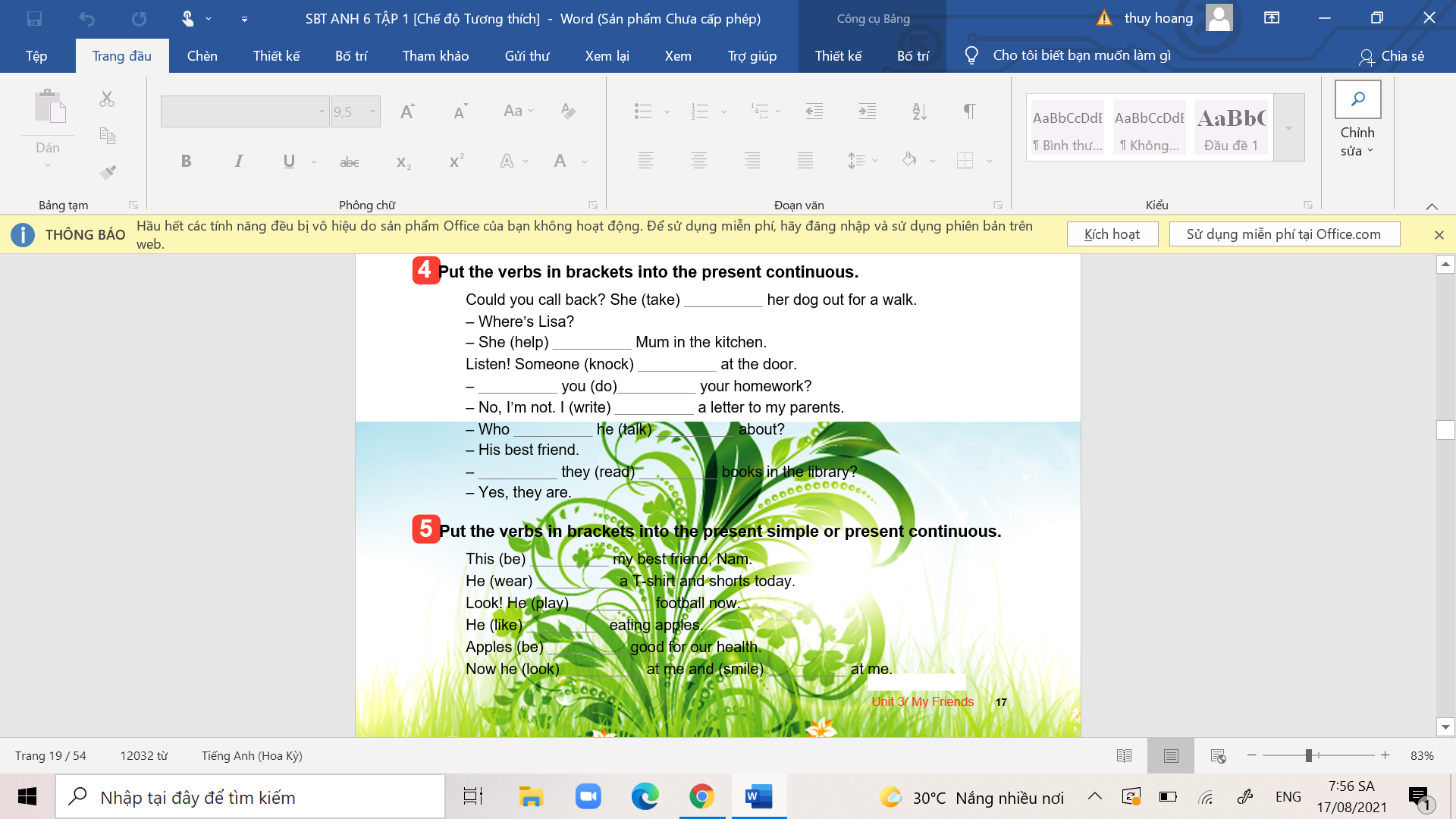 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé.
mình cần gấp ạ!!! mong các bạn giúp ạ ^^
Xem thêm câu trả lời
bài 2, bài 3 ạbài 4, bài 5 ạ mong mn giúp!!! chứ mình hỏi bài đến lần thứ 4 ko ai giúp mình T^T mong các bn giúp mình ạ
Đọc tiếp
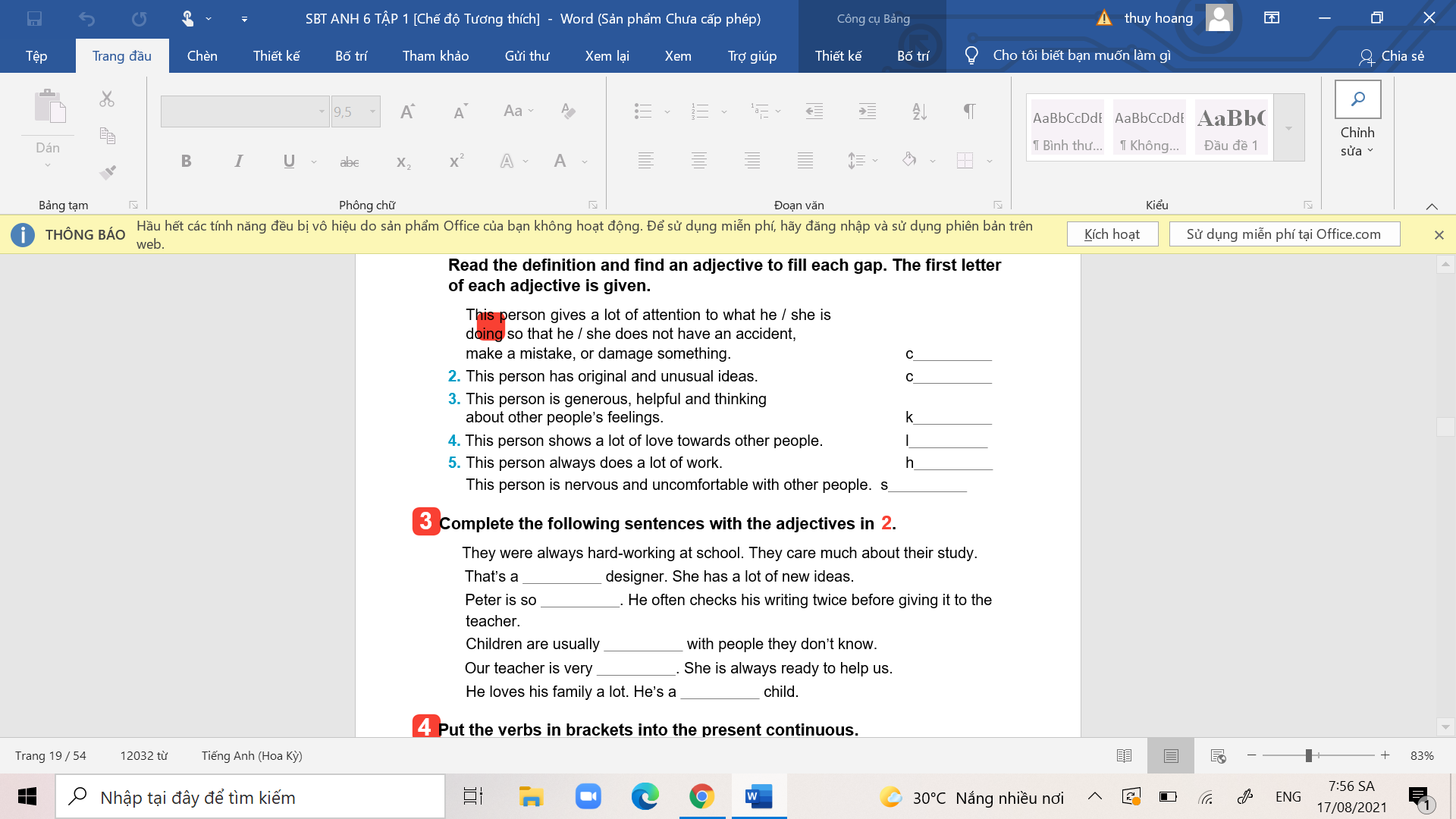 bài 2, bài 3 ạ
bài 2, bài 3 ạ
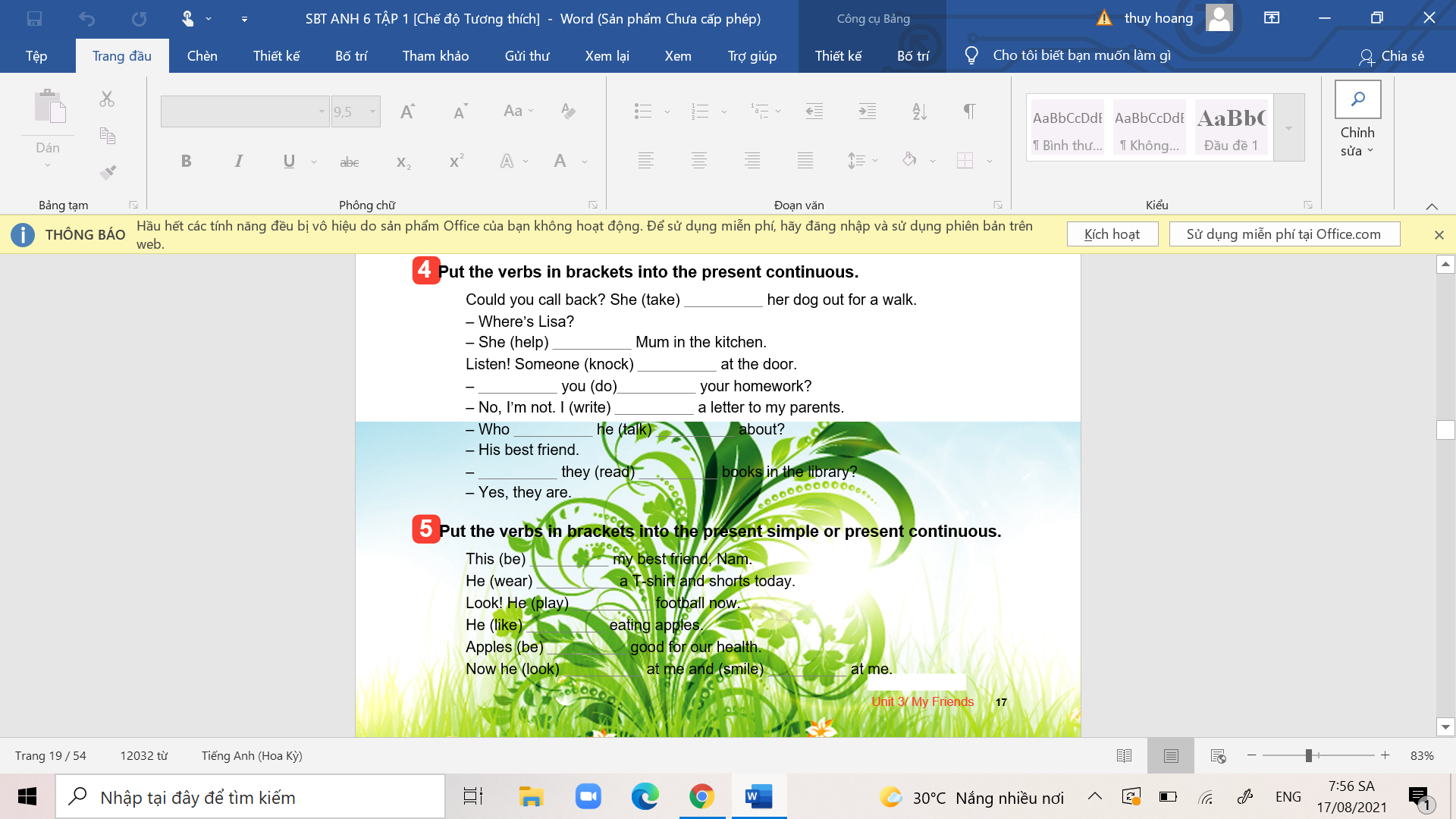
bài 4, bài 5 ạ
mong mn giúp!!! chứ mình hỏi bài đến lần thứ 4 ko ai giúp mình T^T mong các bn giúp mình ạ ![]()
tiêu đề bài hai có nghĩa là j zậy bnnnnnnnnnnnnnnnn
mk nhát đọc đề quá
Đúng 0
Bình luận (1)
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
Đúng 2
Bình luận (3)
giúp giúp mình bài 2 bài 3 với ạ
Đọc tiếp
giúp giúp mình bài 2 bài 3 với
ạ
2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (1)
 ai giúp mình bài số 3 ạ, đang cần gấp ạ, mình cảm ơn
ai giúp mình bài số 3 ạ, đang cần gấp ạ, mình cảm ơn
Giúp mik vs ạ. Mình đang cần gấp ạ!!! Bài 3 ạ

giúp mình bài 3 bài 4 với ạ
lần sau bạn chụp thẳng ra nha,đùng chụp ngang
Đúng 0
Bình luận (0)
 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ
2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
Đúng 2
Bình luận (4)
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)
Đúng 0
Bình luận (0)
Giúp mình bài 3 và bài 4 với ạ 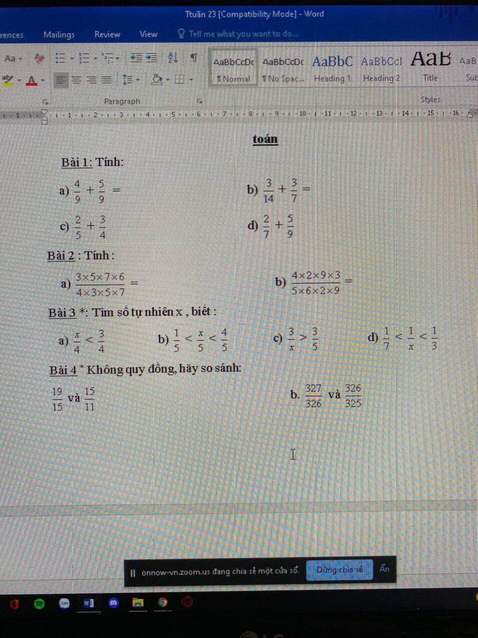
e thay dấu = cho tất cả phsố trog bài 3 rồi tìm x , khi tìm x thì coi dấu của bài r nói x lớn hoặc nhỏ hơn số đó là đc
Đúng 1
Bình luận (0)

























