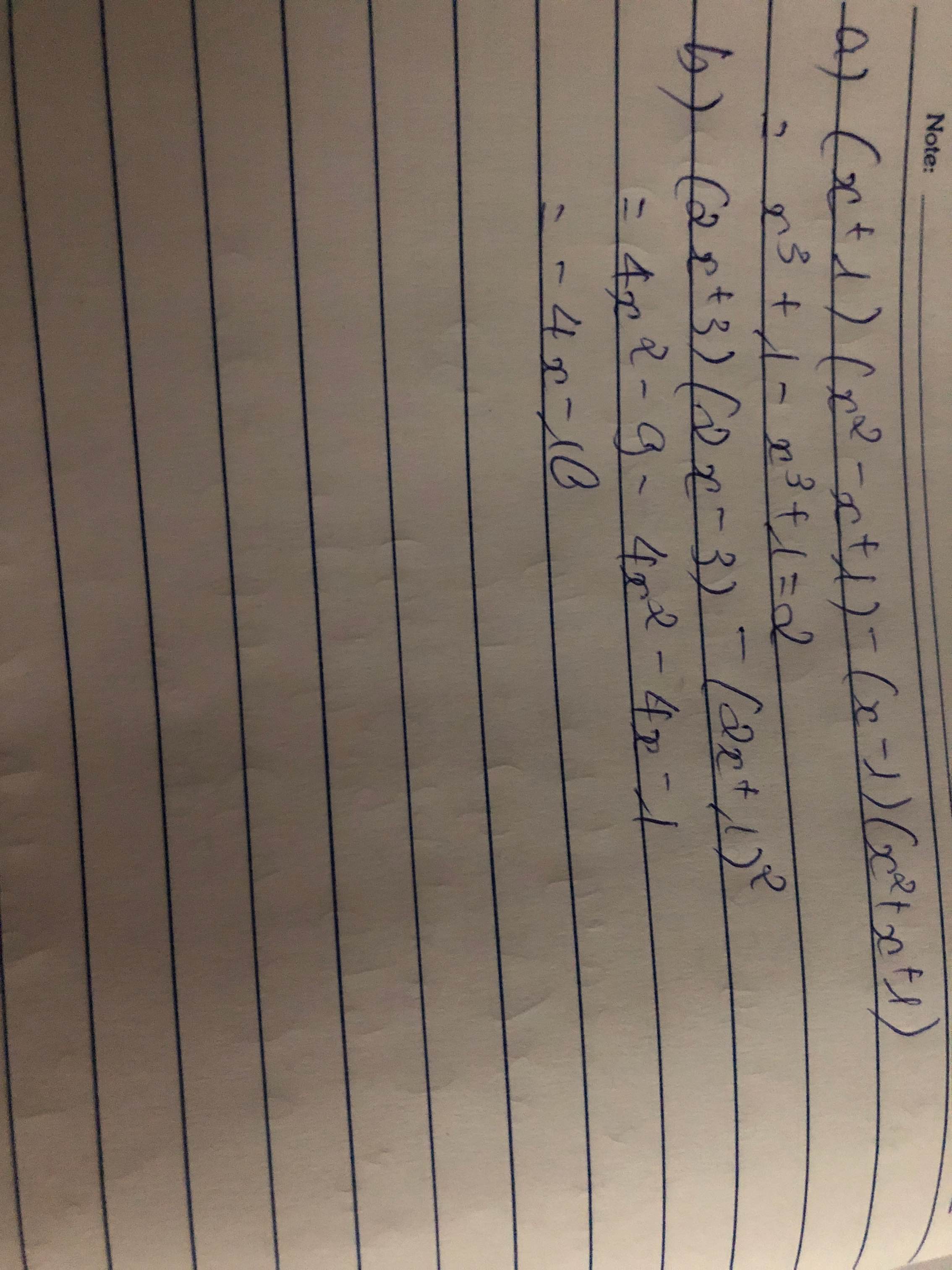Rút gọn: 1+(x + 1/x³+1 - 1/x-x² - 1 -2/x²+1): x³ - 2x²/x² - x² +. x

Những câu hỏi liên quan
Rút gọn biểu thức sau. Với giá trị nào của x, giá trị của biểu thức rút gọn là dương?
(\(\dfrac{\dfrac{x}{x+1}}{\dfrac{x^2}{x^2+x+1}}\) - \(\dfrac{2x+1}{x^2+x}\))\(\dfrac{x^2-1}{x-1}\)
\(\left(\dfrac{\dfrac{x}{x+1}}{\dfrac{x^2}{x^2+x+1}}-\dfrac{2x+1}{x^2+x}\right)\dfrac{x^2-1}{x-1}\)ĐK : \(x\ne\pm1\)
\(=\left(\dfrac{x}{x+1}.\dfrac{x^2+x+1}{x^2}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)=\left(\dfrac{x^2+x-1}{x^2+x}-\dfrac{2x+1}{x\left(x+1\right)}\right)\left(x+1\right)\)
\(=\left(\dfrac{x^2+x-1-2x-1}{x\left(x+1\right)}\right)\left(x+1\right)=\dfrac{x^2-3x-2}{x}\)
Đúng 0
Bình luận (0)
à xin lỗi mình nhầm dòng cuối
\(=\dfrac{x^2-x-2}{x}=\dfrac{\left(x+1\right)\left(x-2\right)}{x}\)
Để biểu thức trên nhận giá trị dương khi
\(\dfrac{\left(x+1\right)\left(x-2\right)}{x}>0\)bạn tự xét TH cả tử và mẫu nhé, mình đánh trên này bị lỗi
Đúng 0
Bình luận (0)
rút gọn
(x + 1) (x2 - x + 1) - (x -1) (x2 + x + 1)
(2x + 3) (2x-3) - (2x+1)2
a) Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3+1-x^3+1\)
=2
b) Ta có: \(\left(2x+3\right)\left(2x-3\right)-\left(2x+1\right)^2\)
\(=4x^2-9-4x^2-4x-1\)
\(=-4x-10\)
Đúng 0
Bình luận (0)
P= (1/x-1 - 2x/ x^3 - x^2 +x -1) : ( 1-2x/x+1) (x khác 0, x khác +1 hoặc -1
a) rút gọn P
\(P=\left(\dfrac{1}{x-1}-\dfrac{2x}{x^3-x^2+x-1}\right):\left(\dfrac{1-2x}{x+1}\right)\left(ĐKXĐ:x\ne0;x\ne\pm1\right)\)
\(=\left(\dfrac{1}{x-1}-\dfrac{2x}{x^2\left(x-1\right)+\left(x-1\right)}\right):\left(\dfrac{1-2x}{x+1}\right)\)
\(=\left(\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\right):\left(\dfrac{1-2x}{x+1}\right)\)
\(=\left(\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\right):\left(\dfrac{1-2x}{x+1}\right)\)
\(=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}:\dfrac{1-2x}{x+1}\)
\(=\dfrac{x-1}{x^2+1}:\dfrac{1-2x}{x+1}\)
\(=\dfrac{x-1}{x^2+1}.\dfrac{x+1}{1-2x}\)
\(=\dfrac{x^2-1}{\left(x^2+1\right)\left(1-2x\right)}\)
Đúng 0
Bình luận (0)
Rút gọn \(\left(\dfrac{1}{x-1}+2+\dfrac{2x^3+x^2-x}{1-x^3}\right):\dfrac{1-2x}{x^3+x-2}\)
ĐKXĐ: \(x\notin\left\{1;\dfrac{1}{2}\right\}\)
\(\left(\dfrac{1}{x-1}+2+\dfrac{2x^3+x^2-x}{1-x^3}\right):\dfrac{1-2x}{x^3+x-2}\)
\(=\left(\dfrac{1}{x-1}+2-\dfrac{2x^3+x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}\right)\cdot\dfrac{x^3+x-2}{1-2x}\)
\(=\dfrac{x^2+x+1+2\left(x^3-1\right)-2x^3-x^2+x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^3-x^2+x^2-x+2x-2}{-\left(2x-1\right)}\)
\(=\dfrac{2x+1+2x^3-2-2x^3}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x^2+x+2\right)}{-\left(2x-1\right)}\)
\(=\dfrac{2x-1}{x^2+x+1}\cdot\dfrac{-\left(x^2+x+2\right)}{2x-1}=\dfrac{-x^2-x-2}{x^2+x+1}\)
Đúng 3
Bình luận (0)
rút gọn biểu thức (x/(x+1)^3.(1/x+1) + 1/x^2+2x+1.(1/x^2+1)): x-1/x^3
có phải ý bạn là:
rút gọn biểu thức:
\(\frac{x}{\left(x+1\right)^3}\cdot\frac{1}{x+1}+\frac{1}{x^2+2x+1}\cdot\frac{1}{x^2+1}:\frac{x-1}{x^3}\)
Đúng 0
Bình luận (0)
2 a. rút gọn biểu C = \(\dfrac{2x^{\text{2}}-x}{\text{x }-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)
b. Rút gọn biểu thức D = \(\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{\text{a}}-1}\right):\dfrac{\sqrt{\text{a}}+1}{a-2\sqrt{a}+1}\)
Vậy khi rút gọn một biểu thức hửu tỉ và một biểu thức chứa căn có tìm điều kiện xác định không?
\(a,C=\dfrac{2x^2-x-x-1+2-x^2}{x-1}\left(x\ne1\right)\\ C=\dfrac{x^2-2x+1}{x-1}=\dfrac{\left(x-1\right)^2}{x-1}=x-1\\ b,D=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\left(a>0;a\ne1\right)\\ D=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
Có
Đúng 1
Bình luận (0)
Rút gọn biểu thức
e) (x+1)2 + (x – 1)2 – 2(1 + x)(1 ![]() x)
x)
f) 2x(2x – 1)2 – 3x(x+3)(x – 3) – 4x(x+1)2
g) 3(x + 2)2 – (3x + 1)(x + 5) + (x + 5)2
f: Ta có: \(2x\left(2x-1\right)^2-3x\left(x+3\right)\left(x-3\right)-4x\left(x+1\right)^2\)
\(=2x\left(4x^2-4x+1\right)-3x\left(x^2-9\right)-4x\left(x^2+2x+1\right)\)
\(=8x^3-8x^2+2x-3x^3+27x-4x^3-8x^2-4x\)
\(=x^3-16x^2+25x\)
g: Ta có: \(3\left(x+2\right)^2-\left(3x+1\right)\left(x+5\right)+\left(x+5\right)^2\)
\(=3\left(x^2+4x+4\right)-\left(3x^2+16x+5\right)+x^2+10x+25\)
\(=3x^2+12x+12-3x^2-16x-5+x^2+10x+25\)
\(=x^2+6x+32\)
Đúng 3
Bình luận (0)
e) (x+1)2+(x-1)2-2(1+x)(1-x)
= (x+1)2 + 2(1+x)(x-1) + (x-1)2
= (x+1+x-1)2
= 4x2
Đúng 0
Bình luận (0)
a: Ta có: \(\left(x+1\right)^2+\left(x-1\right)^2-2\left(1+x\right)\left(1-x\right)\)
\(=\left(x+1\right)^2+2\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\)
\(=\left(x+1+x-1\right)^2\)
\(=4x^2\)
c: Ta có: \(3\left(x+2\right)^2-\left(3x+1\right)\left(x+5\right)+\left(x+5\right)^2\)
\(=3x^2+12x+12-3x^2-16x-5+x^2+10x+25\)
\(=x^2+6x+32\)
Đúng 1
Bình luận (0)
1, rút gọn biểu thứca, [(3x - 2)(x + 1) - (2x + 5)(x2 - 1)] : (x + 1)b, (2x + 1)^2 - 2(2x + 1)(3 - x) + (3 - x)^2c, (x - 1)^3 - (x + 1) (x2 - x + 1) - (3x + 1)(1 - 3x)
a: \(=\dfrac{\left(x+1\right)\left[\left(3x-2\right)-\left(2x+5\right)\left(x-1\right)\right]}{x+1}\)
=3x-2-2x^2+2x-5x+5
=-2x^2+3
b: \(=\left(2x+1-3+x\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)
c: =x^3-3x^2+3x-1-x^3-1+9x^2-1
=6x^2+3x-3
Đúng 1
Bình luận (0)
\(a,\left[\left(3x-2\right)\left(x+1\right)-\left(2x+5\right)\left(x^2-1\right)\right]:\left(x+1\right)\)
\(=\left[\left(3x-2\right)\left(x+1\right)-\left(2x+5\right)\left(x-1\right)\left(x+1\right)\right]:\left(x+1\right)\)
\(=\left[\left(x+1\right)\left(3x-2-\left(2x+5\left(x-1\right)\right)\right)\right]:\left(x+1\right)\)
\(=\left[\left(x+1\right)\left(3x-2-2x^2+2x-5x+5\right)\right]:\left(x+1\right)\)
\(=\left[\left(x+1\right)\left(-2x^2+3\right)\right].\dfrac{1}{x+1}\)
\(=-2x^2+3\)
\(b,\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)\)
\(=\left(2x+1\right)\left[\left(2x+1\right)-2\left(3-x\right)\right]\)
\(=\left(2x+1\right)\left(2x+1-6+2x\right)\)
\(=\left(2x+1\right)\left(4x-5\right)\)
\(c,\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(3x+1\right)\left(1-3x\right)\)
\(=x^3-3x^2+3x-1-x^3-1-\left(3x-9x^2+1-3x\right)\)
\(=-3x^2+3x-2-3x+9x^2-1+3x\)
\(=6x^2+3x-3\)
Đúng 1
Bình luận (0)
BÀI 1cho biểu thức
P= (2√x+xx√x−1−1√x−1):(1−√x+2x+√x+1)(2x+xxx−1−1x−1):(1−x+2x+x+1)
a) Rút gọn P
b) tính √PP khi x=5+2√3