CMR: xy mũ 3 - yx mũ 3 chia hết cho 6
cho a,b,c,d thuộc z và (a+b+c+d) chia hết co 6
cmr : ( a mũ 3 + b mũ 3 + c mũ 3 + d mũ 3) chia hết cho 6
Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
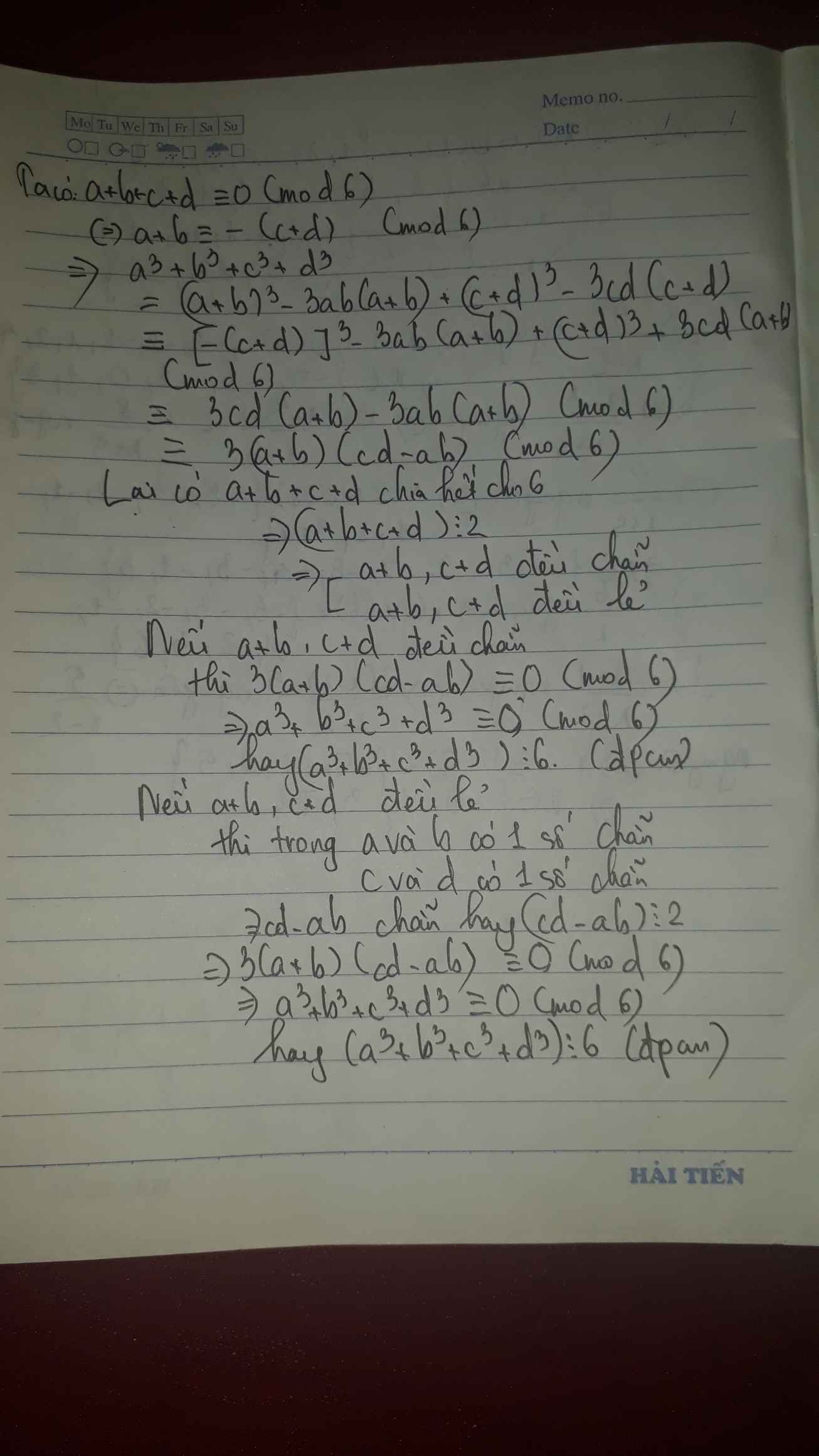
cho a,b,c,d thuộc z và (a+b+c+d) chia hết co 6
cmr : ( a mũ 3 + b mũ 3 + c mũ 3 + d mũ 3) chia hết cho 6
cmr với n là số tn thì
a)2 nhân n mũ 3 +n chia hết cho 3.
b)n nhân (5n cộng 3) nhân (2n mũ 2 cộng 1) chia hết cho 6.
c) cho số tn a,b,c. chứng minh rằng a mũ 3 cộng b mũ 3 cộng c mũ 3 chia hết cho 6 thì a cộng b cộng c chia hết cho 6 và ngược lại, nếu a +b+c chia hết cho 6 thì a mũ 3 +b mũ 3+c mũ 3 cũng chia hết cho 6
bài 5 : cmr : a, x thuộc z thì ( x mũ 3 - 13x ) chia hết cho 6
b, ( x mũ 3 + 41x) chia hết cho 6
a) Ta có: x\(^3\)-13x = \(x^3\)-x-12x = x(x\(^2\)-1) -12x = (x+1)x(x-1) -12x chia hết cho 6 vì
(x+1)x(x-1) là tích của 3 số nguyên liên tiếp nên chia hết cho 6
b) Ta có: x\(^3\)+41x = x\(^3\)-x+42 = ...
bài 5 : cmr : a, x thuộc z thì ( x mũ 3 - 13x ) chia hết cho 6
b, ( x mũ 3 + 41x) chia hết cho 6
cmr s=2+2 mũ 2 +2 mũ 3 + 2 mũ 4 + 2 mũ 5 + 2 mũ 6 + 2 mũ 7 + 2 mũ 8 chia hết cho -6
S =
2 + (2^2) + (2^3) + (2^4) + (2^5) + (2^6) + (2^7) + (2^8) =| 510 |
S =
2 + (2^2) + (2^3) + (2^4) + (2^5) + (2^6) + (2^7) + (2^8) =
| 510 |
CMR
n mũ 3-13n chia hết cho 6
n mũ 3+3n mũ 2+2n chia hết cho 6
n mũ 5-n chia hết cho 5
n lớn hơn 3 lớn hơn n nguyên tố
CM [n mũ 2-1] chia hết cho 24
n*[n+2]*25n mũ 2 chia hết cho 24
\(n^3-13n=n\left(n^2-1\right)-12n.\)
\(=n\left(n-1\right)\left(n-2\right)-12n\)
Vậy chia hết cho 6 vì
n(n-1)(n-2) chia hết cho 2;3 => chia hết cho 6
12n chia hết cho 6
Cho a,b,c là các số nguyên. CMR: a) a mũ 3 -a chia hết cho 6
b) a mũ 3+b mũ 3+c mũ 3 chia hết cho 6 khi và chỉ khi a+b+c chia hết cho 6
Mình cần gấp,mình đang học đến bài phân tích đa thức thành nt
a: \(a^3-a=a\left(a-1\right)\left(a+1\right)\)
Vì a;a-1;a+1 là ba số nguyên liên tiếp
nên \(a\left(a-1\right)\left(a+1\right)⋮3!\)
hay \(a^3-a⋮6\)
cho A= 2+2 mũ 2+ 2 mũ 3+...+2 mũ 60
cmr: A chia hết cho 6
\(A=2+2^2+2^3+\dots+2^{60}\\=(2+2^2)+(2^3+2^4)+(2^5+2^6)+\dots+(2^{59}+2^{60})\\=6+2^2\cdot(2+2^2)+2^4\cdot(2+2^2)+\dots+2^{58}\cdot(2+2^2)\\=6+2^2\cdot6+2^4\cdot6+\dots+2^{58}\cdot6\\=6\cdot(1+2^2+2^4+\dots+2^{58})\)
Vì \(6\cdot(1+2^2+2^4+\dots+2^{58})\vdots6\)
nên \(A\vdots6\)