a: \(50=2\cdot5^2;75=5^2\cdot3\)

=>\(ƯCLN\left(50;75\right)=5^2=25\)

=>\(ƯC\left(50;75\right)=Ư\left(25\right)=\left\{1;5;25\right\}\)

\(x\inƯC\left(50;75\right)\)

=>\(x\in\left\{1;5;25\right\}\)

mà x<=20

nên \(x\in\left\{1;5\right\}\)

b: \(35=5\cdot7;105=3\cdot5\cdot7\)

=>\(ƯCLN\left(35;105\right)=5\cdot7=35\)

\(35⋮x;105⋮x\)

=>\(x\inƯC\left(35;105\right)\)

=>\(x\inƯ\left(35\right)\)

=>\(x\in\left\{1;5;7;35\right\}\)

mà x>5

nên \(x\in\left\{7;35\right\}\)

c: \(144=2^4\cdot3^2;192=2^6\cdot3;240=2^4\cdot3\cdot5\)

=>\(ƯCLN\left(144;192;240\right)=2^4\cdot3=48\)

\(144⋮x;192⋮x;240⋮x\)

=>\(x\inƯC\left(144;192;240\right)\)

mà x lớn nhất

nên x=ƯCLN(144;192;240)=48

d: \(54=3^3\cdot2;14=2\cdot7\)

=>\(ƯCLN\left(54;14\right)=2\)

\(x\inƯC\left(54;14\right)\)

mà x lớn nhất

nên x=ƯCLN(54;14)

=>x=2

bấm máy tính là ra

Ta có: 

\(40=2^3.5\)

\(75=3.5^2\)

\(105=3.5.7\)

\(ƯCLN\left(40;75;105\right)=5\)

\(BCNN\left(40;75;105\right)=2^3.3.5^2.7=8.3.25.7=4200\)

Ta có :

40 = 2³ . 5

75 = 3 . 5²

105 = 3 . 5 .7

ƯCLN(40;75;105) = 5 . 3 = 15

BCNN(40;75;105) = 2³ . 5² . 3 . 7 = 4200

--thodagbun--

( h tớ lm b mt nè :( )

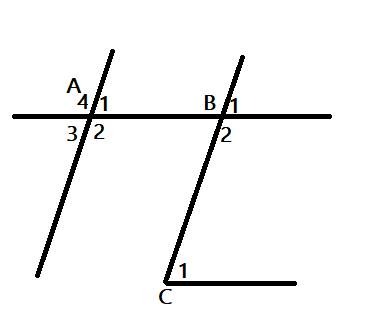
Để giải thích tại sao Cx // Bt và Az // By, chúng ta cần xem xét các góc đã cho và quan sát các quy tắc và định lý liên quan đến góc và đường thẳng trong hình học.

a) Cx // Bt: Theo giả thiết, C1^ = 75 độ và A4^ = 105 độ. Ta biết rằng trong một tam giác, tổng các góc trong một tam giác bằng 180 độ. Vì vậy, B1^ = 180^ - C1^ = 180^ - 75^ = 105^.

Theo quy tắc, nếu hai góc cùng nằm bên trái hoặc cùng nằm bên phải của một đường chéo và chúng có cùng độ lớn, thì các cặp đường thẳng song song với nhau. Trong trường hợp này, C1^ và B1^ đều nằm bên trái của đường chéo và có cùng độ lớn 105 độ. Vì vậy, chúng ta có Cx // Bt.

b) Az // By: Theo giả thiết, C1^ = 75 độ và 132^ = 105 độ. Tương tự như trên, ta có B2^ = 180^ - 132^ = 48^.

Chúng ta cũng biết rằng hai góc đối nhau của một hình chữ Z có cùng độ lớn. Trong trường hợp này, A4^ và B2^ là hai góc đối nhau của hình chữ Z và cùng có độ lớn 105 độ. Vì vậy, chúng ta có Az // By.

Tóm lại, chúng ta có Cx // Bt do C1^ = B1^ và Az // By do A4^ = B2^.

Ta có : 

40 = 2³ . 5 (1)

75 = 3 . 5² (2)

105 = 3 . 5 . 7 (3)

Từ (1), (2) và (3) => ƯCLN (A ; B ; C) = 5

                            => BCNN (A ; B ; C) = 2³ . 3 . 5² . 7 = 4200

Vậy ... 

~Study well~

#KSJ

a) 220 = 2² . 5 . 11

240 = 2⁴ . 3 . 5

300 = 2² . 3 . 5²

=> ƯCLN(220;240;300) = 2² . 5 . 3 = 60

=> BCNN(220;240;300) = 2⁴ . 5 . 11 . 3 = 2640

b) 40 = 2³ . 5

75 = 3 . 5²

105 = 3 . 5 .7

=> ƯCLN(40;75;105) = 5 . 3 = 15

=> BCNN(40;75;105) = 2³ . 5² . 3 . 7 = 4200

c) 18 = 2 . 3²

36 = 2² . 3²

72 = 2³ . 3²

=> ƯCLN(18;36;72) = 2 . 3² = 18

=> BCNN(18;36;72) = 2³ . 3² = 72

bấm casio đi

mình cảm ơn nha

a) Ta có: 18=2⋅3^21

24=2^3⋅3

30=2⋅3⋅5

Do đó: ƯCLN(18;24;30)=2⋅3=6 và BCNN(18;24;30)=2^3⋅3^2⋅5=360

b) Ta có: 40=2^3⋅5

75=3⋅5^2

105=3⋅5⋅7105=3⋅5⋅7

Do đó: ƯCLN(40;75;105)=5^1=5 và BCNN(40;75;105)=2^3⋅3⋅5^2⋅7=4200

c) Ta có: 18=2⋅3^2

36=2^2⋅3^2

72=2^3⋅3^2

Do đó: ƯCLN(18;36;72)=2.3^2=2⋅9=18 và BCNN(18;36;72)=2^3⋅3^2=72

Chọn A