a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím

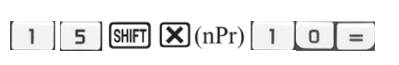
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)

b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím

 Thì ta nhận được kết quả là 495

c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím

Thì ta được kết quả là 1150

(-123) + (-18) = - 141                   

(-375) + 210 = - 165 

(-127) + 25 + (-136) = - 238

(-123)+(-18)=-(123+18)=-141

(-375)+210=210-375=-165

(-127)+25+(-136)=-127-136+25=-238

a) \(\tan ( - {75^ \circ }) =  - 2 - \sqrt 3 \)

b) \(\cot \left( { - \frac{\pi }{5}} \right) \approx  - 1,376\)

a) \(C_7^2 = \frac{{7!}}{{2!.5!}} = \frac{{7.6}}{2} = 21\)

b) \(C_9^0 + C_9^9 = \frac{{9!}}{{0!.9!}} + \frac{{9!}}{{9!.0!}} = 2\)

c) \(C_{15}^3 - C_{14}^3 = \frac{{15!}}{{3!.12!}} - \frac{{14!}}{{3!.11!}} = \frac{{15.14.13}}{{3.2.1}} - \frac{{14.13.12}}{{3.2.1}} = 91\)

Ta có: \((C_{15}^{12} + C_{15}^{13} )+ C_{16}^{14} = C_{16}^{13} + C_{16}^{14} = C_{17}^{14} = 680\)

Tóm tắt

\(V=2l\Rightarrow m=2kg\)

\(t_1=25^0C\)

\(t_2=100^0C\)

\(c=4200J/kg.K\)

________________

\(Q=?\)

Giải

Nhiệt lượng cần thiết để đun sôi nước là:

\(Q=m.c.\left(t_2-t_1\right)=2.4200.\left(100-25\right)=630000\left(J\right)\)

👉 Điều này xảy ra khi:

\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. = \emptyset\)

→ Tức là:

\(m \leq 3 m + 1\)

Giải bất phương trình:

\(m \leq 3 m + 1 \Rightarrow - 2 m \leq 1 \Rightarrow m \geq - \frac{1}{2}\)

Tức là: phải có phần tử chung giữa \(A = \left(\right. - \infty ; m \left.\right)\) và \(B = \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\)

→ Tức là:

\(\left(\right. - \infty ; m \left.\right) \cap \left[\right. 3 m + 1 ; 3 m + 2 \left]\right. \neq \emptyset\)

→ Điều này xảy ra khi tồn tại \(x \in \left[\right. 3 m + 1 ; 3 m + 2 \left]\right.\) sao cho \(x < m\)

→ Nói cách khác:

\(3 m + 1 < m\)

Giải bất phương trình:

\(3 m + 1 < m \Rightarrow 2 m < - 1 \Rightarrow m < - \frac{1}{2}\)

⛔ Hai điều kiện mâu thuẫn nhau → Không có giá trị \(m\) nào thỏa mãn đồng thời cả hai điều kiện.

1và 1/12 bằng bao nhiêu

Yêu cầu $A \subset \mathrm{C}_{\mathbb{R}}B$ nghĩa là mọi phần tử thuộc $A$ đều phải thuộc $\mathrm{C}_{\mathbb{R}}B$.

Ta có:

Để $A \subset \mathrm{C}_{\mathbb{R}}B$, ta cần tập $A$ phải nằm hoàn toàn trong một trong hai khoảng của $\mathrm{C}_{\mathbb{R}}B$, hoặc nằm "vắt ngang" qua chúng (nhưng vì $A$ là nửa đường thẳng mở về $-\infty$ nên trường hợp này không xảy ra).

$A \subset \mathrm{C}_{\mathbb{R}}B \iff \text{mọi } x \in (-\infty; m) \text{ thì } x \in (-\infty; 3m+1) \cup (3m+2; +\infty)$.

Xem xét vị trí của $A$: $(-\infty; m)$.

Vậy, điều kiện để $A \subset \mathrm{C}_{\mathbb{R}}B$ là $m \ge -\frac{1}{2}$.

Yêu cầu $\mathrm{C}_{\mathbb{R}}A \cap B \neq \emptyset$ nghĩa là hai tập hợp này phải có phần tử chung.

Ta có:

Để hai tập hợp này có giao khác rỗng, giá trị nhỏ nhất của một tập phải $\le$ giá trị lớn nhất của tập còn lại.

Vì $B$ là một đoạn hữu hạn, ta chỉ cần $\mathrm{C}_{\mathbb{R}}A$ "chạm" vào hoặc "chồng lấn" với $B$.

Điều kiện $\mathrm{C}_{\mathbb{R}}A \cap B \neq \emptyset$ xảy ra khi và chỉ khi:

Vì $\mathrm{C}_{\mathbb{R}}A = [m; +\infty)$ không có cận trên hữu hạn, nên ta chỉ xét điều kiện thứ nhất:

Vậy, điều kiện để $\mathrm{C}_{\mathbb{R}}A \cap B \neq \emptyset$ là $m \ge -1$.

a) 3,14.7,652 = 24,02728

b) (-10,3125): 2,5 = -4,125

c) 54,369 : (-4,315) = -12,6

a)3,14.7,652=24,02728

b)(-10,3125):2,5=-4,125

c)54,369:(-4,315)=-12,6

a) \({(3,147)^3} \approx 31,167\)

b) \({( - 23,457)^5} \approx  - 7\,101\,700,278\)

c) \({\left( {\frac{4}{{ - 5}}} \right)^4} = \frac{{256}}{{625}}\);

d) \({(0,12)^2} \cdot {\left( {\frac{{ - 13}}{{28}}} \right)^5} \approx  - 3,{107.10^{ - 4}}\).