Trên sông, một cano chuyển động thẳng đều theo hướng \(S{15^o}E\) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.

Những câu hỏi liên quan
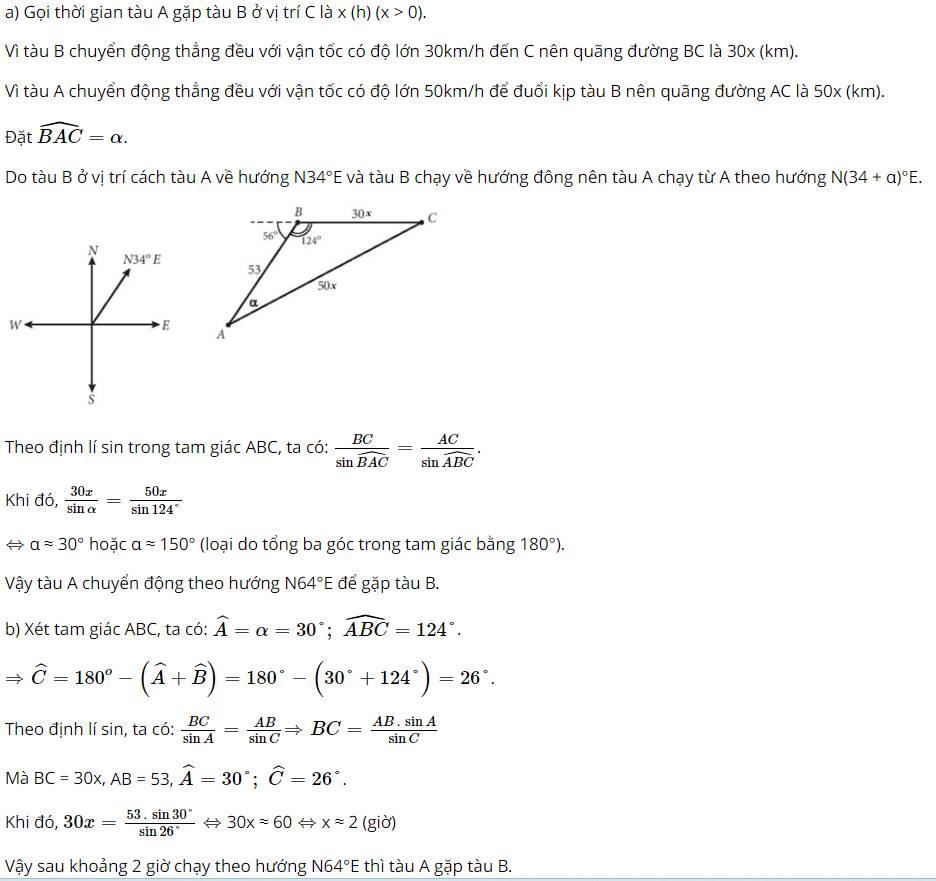
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \(N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông, đồng thời tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để gặp tàu B.
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A gặp tàu B?
a)
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.
Đúng 0
Bình luận (0)
bài 1:khúc sông AB dài 54km , một cano đi từ A tới B rồi quay về A.khi đi dòng sông nc yên lặng,khi về nhờ có nc chảy ( theo hướng B đến A0 nên cano đã đến sớm hơn lúc đi là 12p ,tính vận tốc cano lúc nc yên lặng biết vận tốc nc chảy là 3km/hbài 2 :hai vật chuyển động trên 1 đường tròn có đường kính 20m xuất phát cùng 1 lúc , từ cùng một điểm , nếu chuyển động cùng chiều thì sau 20 giây sẽ lại gặp nhau , nếu chuyển động ngược chiều thì sau 4 gây lại gặp nhau , tính vận tốc mỗi vật
Đọc tiếp
bài 1:
khúc sông AB dài 54km , một cano đi từ A tới B rồi quay về A.khi đi dòng sông nc yên lặng,khi về nhờ có nc chảy ( theo hướng B đến A0 nên cano đã đến sớm hơn lúc đi là 12p ,tính vận tốc cano lúc nc yên lặng biết vận tốc nc chảy là 3km/h
bài 2 :hai vật chuyển động trên 1 đường tròn có đường kính 20m xuất phát cùng 1 lúc , từ cùng một điểm , nếu chuyển động cùng chiều thì sau 20 giây sẽ lại gặp nhau , nếu chuyển động ngược chiều thì sau 4 gây lại gặp nhau , tính vận tốc mỗi vật
Bài 1:
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x
⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625,
√∆’ = 25
x1 = 5 – 25 = -20,
x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Vậy Vận tốc của xuồng khi đi là 30 km/h
Đúng 0
Bình luận (0)
Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt nên :
4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt
Đúng 0
Bình luận (0)
Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s) ( x> y >0 )
Vì khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường mà vật đi nhanh hơn đi được trong 20 giây hơn quãng đường của vật kia đi trong 20 giây là đúng 1 vòng ( 20 cm) \(20x-20y=20\pi\)
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng \(4x+4y=20\pi\)
Từ \(20x-20y=20\pi\)và \(4x+4y=20\pi\)
Ta có hệ phương trình như sau:
\(\hept{\begin{cases}20x-20y=20\pi\\4x+4y=20\pi\end{cases}\Leftrightarrow\hept{\begin{cases}20\left(x+y\right)=20\pi\\4\left(x+y\right)=20\pi\end{cases}}}\)\(\Leftrightarrow\hept{\begin{cases}x-y=\pi\\x+y=5\pi\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\pi\\y=2\pi\end{cases}}}\)
Vậy...................................
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1:khúc sông AB dài 54km , một cano đi từ A tới B rồi quay về A.khi đi dòng sông nc yên lặng,khi về nhờ có nc chảy ( theo hướng B đến A0 nên cano đã đến sớm hơn lúc đi là 12p ,tính vận tốc cano lúc nc yên lặng biết vận tốc nc chảy là 3km/hbài 2 :hai vật chuyển động trên 1 đường tròn có đường kính 20m xuất phát cùng 1 lúc , từ cùng một điểm , nếu chuyển động cùng chiều thì sau 20 giây sẽ lại gặp nhau , nếu chuyển động ngược chiều thì sau 4 gây lại gặp nhau , tính vận tốc mỗi vật
Đọc tiếp
bài 1:
khúc sông AB dài 54km , một cano đi từ A tới B rồi quay về A.khi đi dòng sông nc yên lặng,khi về nhờ có nc chảy ( theo hướng B đến A0 nên cano đã đến sớm hơn lúc đi là 12p ,tính vận tốc cano lúc nc yên lặng biết vận tốc nc chảy là 3km/h
bài 2 :hai vật chuyển động trên 1 đường tròn có đường kính 20m xuất phát cùng 1 lúc , từ cùng một điểm , nếu chuyển động cùng chiều thì sau 20 giây sẽ lại gặp nhau , nếu chuyển động ngược chiều thì sau 4 gây lại gặp nhau , tính vận tốc mỗi vật
Bài 1:Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: (giờ)
Theo đầu bài có phương trình: + 1 =
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
Đúng 0
Bình luận (0)
--Gọi vận tốc của 2 vật là x1 , x2 ( giả sử x1 > x2 > 0 )
--khi chạy ngược chiều S = ( x1 + x2 ) . t = 4 ( x1 + x2 )
--Khi chạy cùng chiều : S = ( x1 -- x2 ) t = 20 ( x1 --x2 )
khi chạy ngược chiều , quãng đường 2 vật đi = 1 chu vi đường tròn , khi chạy cùng chiều thì khoảng cách vật 1 cần đuổi kịp vật 2 cũng =1 chu vi đt
nên : 4 ( x1 + x2 ) = 2 pi R VÀ 20 ( x1 -- x2 ) = 2pi R
giải pt ta được : x1 = 3 pi R/ 10 và x2 = pi R /5
với pi = 3,14... và R là bán kính đt
tk nha
Đúng 0
Bình luận (0)
hai bên sông a và b cách nhau 42km dòng sông chảy theo hướng từ a đến b với vận tốc 2,5km/h. Một chiếc cano chuyển động đều từ a về b hết 1h30ph hỏi cano đi ngược từ b về a trong bao lâu
dòng sông chảy theo hướng A->B với \(v=2,5km/h\)
=> đây là vận tốc dòng nước
đổi \(1h30'=\dfrac{3}{2}h\)
\(=>v1=\dfrac{S}{t}=\dfrac{42}{\dfrac{3}{2}}=28km/h\)
mà ca nô đi từ A->B với vận tốc \(v1=28=vc+v=vc+2,5=>vc=v1-v=28-2,5\)\(=25,5km/h\)
đây là vận tốc thực ca nô
đi từ B->A \(=>v2=vc-2,5=25,5-2,5=23km/h\)
\(=>t1=\dfrac{S}{v2}=\dfrac{42}{23}\approx1,8h\)
Đúng 2
Bình luận (0)
Một cano chuyển động với vận tốc 60km/h, dòng nước chảy với vận tốc 15km/h. Tính vận tỗc của cano đối với bờ sông trong các trường hợp sau :
a) Cano chuyển động cùng chiều với dòng nước
b) Cano chuyển động ngược chiều với dòng nước
c) Cano chuyển động vuông góc với dòng nước
Gọi \(\overrightarrow{v_{12}},\overrightarrow{v_{23}}\) lần lượt là vận tốc của cano so với nước , của nước so với bờ
a. Khi cano chuyển động cùng chiều với dòng nước
\(v_{13}=v_{12}+v_{23}=60+15=75\left(km/h\right)\)
b. Khi cano chuyển động ngược chiều với dòng nước
\(v_{13}=v_{12}-v_{23}=60-15=45\left(km/h\right)\)
c. Khi cano chuyển động vuông góc với nước
\(v_{13}=\sqrt{v_{12}^2+v_{23}^2}=\sqrt{60^2+15^2}=15\sqrt{17}\approx62\left(km/h\right)\)
Đúng 2
Bình luận (0)
giải bài tập lý 8 một ca nô xuất phát từ bến sông A có vận tốc với nước là 12 km/h (vận tốc riêng của ca nô) đuổi theo một xalan có vận tốc đối với bờ là 10km/h(vận tốc riêng+ vận tốc nước chảy) xuất phát trước 2h từ bến sông B trên cùng một dòng sông . ca nô và xà lan đều chạy xuôi dòng theo hướng AB. khi chạy ngang qua bến B ca nô tăng gấp đôi vận tốc và sau 3h đuổi kịp xà lan. biết AB60km.hãy xác định vận tốc nước chảy.
Đọc tiếp
giải bài tập lý 8 " một ca nô xuất phát từ bến sông A có vận tốc với nước là 12 km/h (vận tốc riêng của ca nô) đuổi theo một xalan có vận tốc đối với bờ là 10km/h(vận tốc riêng+ vận tốc nước chảy) xuất phát trước 2h từ bến sông B trên cùng một dòng sông . ca nô và xà lan đều chạy xuôi dòng theo hướng AB. khi chạy ngang qua bến B ca nô tăng gấp đôi vận tốc và sau 3h đuổi kịp xà lan. biết AB=60km.hãy xác định vận tốc nước chảy.
Một người xuôi trên khúc Sông dài 60 km, sau đó chuyển hàng hóa mất 30 phút rồi ngược khúc sông 40 km thì mất 6 giờ.Biết vận tốc dòng nước là 2 km/h. Tính vận tốc riêng của cano
Một chiếc phà đi ngang qua một con sông vectơ vận tốc của phà hướng vuông góc với vận tốc dòng chảy và có độ lớn bằng 8km/h. Nếu vận tốc của chiếc phà so với bờ là 10km/h thì vận tốc chảy của nước là
A. 6km/h
B. 8km/h
C. 10km/h
D. 128km/h
Đáp án A
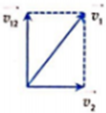
Coi chiếc phà là (1), nước là (2)
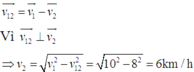
Đúng 0
Bình luận (0)
Một cano dự định đi xuôi dòng từ A đến B rồi quay về A. Biết vận tốc của cano là 15km/h, vận tốc của dong nước là 3km/h, quãng sông AB dài 24km.a. Tính thời gian chuyển động của cano theo dự địnhb. Tuy nhiên trên đường quay về A sau khi đi được quãng đường 7,2 km thì máy hỏng và sau 24 phút thì sửa xong. Hỏi về A đúng dự định thì sau đó cano phải đi với vận tốc là bao nhiêu
Đọc tiếp
Một cano dự định đi xuôi dòng từ A đến B rồi quay về A. Biết vận tốc của cano là 15km/h, vận tốc của dong nước là 3km/h, quãng sông AB dài 24km.
a. Tính thời gian chuyển động của cano theo dự định
b. Tuy nhiên trên đường quay về A sau khi đi được quãng đường 7,2 km thì máy hỏng và sau 24 phút thì sửa xong. Hỏi về A đúng dự định thì sau đó cano phải đi với vận tốc là bao nhiêu