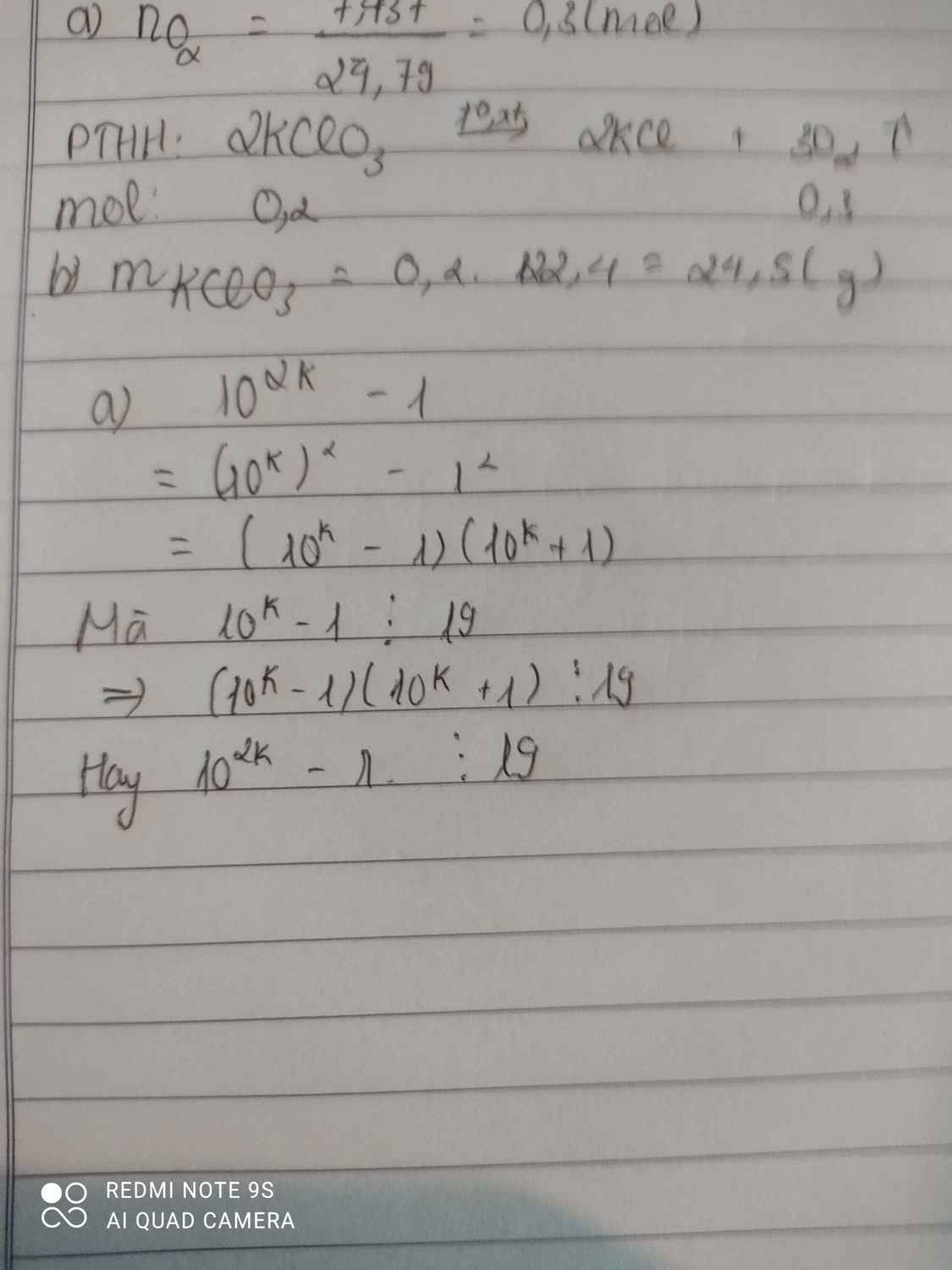\(CMR:a^{2k+1}+b^{2k+1}⋮a+b\left(k\in N;a,b\in N\cdot\right)\)

Những câu hỏi liên quan
Chứng minh rằng từ tỉ lệ thức \(\frac{\left(a^{2k}+b^{2k}\right)}{c^{2k}+d^{2k}}=\frac{a^{2k}-b^{2k}}{c^{2k}-d^{2k}}\left(k\in N\right)\)
Ta có thể suy ra \(\frac{a}{b}=+-\frac{c}{d}\)
Áp dụng t/c của dãy tỉ số bằng nhau ta có \(\frac{\left(a^{2k}+b^{2k}\right)}{c^{2k}+d^{2k}}=\frac{a^{2k}-b^{2k}}{c^{2k}-d^{2k}}=\frac{\left(a^{2k}+b^{2k}\right)+\left(a^{2k}-b^{2k}\right)}{\left(c^{2k}+d^{2k}\right)+\left(c^{2k}-d^{2k}\right)}=\frac{\left(a^{2k}+b^{2k}\right)-\left(a^{2k}-b^{2k}\right)}{\left(c^{2k}+d^{2k}\right)-\left(c^{2k}-d^{2k}\right)}\)
=> \(\frac{a^{2k}}{c^{2k}}=\frac{b^{2k}}{d^{2k}}\) => \(\left(\frac{a}{c}\right)^{2k}=\left(\frac{b}{d}\right)^{2k}\) => \(\frac{a}{c}=\frac{b}{d}\) hoặc \(\frac{a}{c}=-\frac{b}{d}\) ( do số mũ 2k chẵn)
=> \(\frac{a}{b}=\frac{c}{d}\) hoặc \(\frac{a}{b}=-\frac{c}{d}\)
Đúng 0
Bình luận (0)
Bài 1:Cho a,b,c thuộc Q thỏa mãn abc1CMR: 1/ab+a+1+b/bc+b+1+1/abc+bc+b1Bài 2:a)1/2+1/3+2/3+1/4+2/4+3/4+...+1/n+2/n+...+n-/n(với n thuộc Z n2)b)1/2-1/3-2/3+1/4+2/4+3/4-...-1/2k+1-2/2k+1-...-2k/2k+1(k thuộc N,k1)c)1/2-1/3-2/3+1/4+2/4+3/4-...+1/2k+2/2k+...+2k-1/2k(k thuộc N , k1)Bài 3:a)CMr 1/n-1/n+11/n(n+1) (với n thuộc N*)b)1/n(n+1)-1/(n+1)(n+2)2/n(n+1)(n+2)c)-1-1/3-1/6-1/10-1/15-1/21-1/28-1/36-1/45d)1/1.2.3+1/2.3.4+1/3.4.5+...+1/18.19.20Bài 4:Cho các số hữu tỉ a1,a2,.....a9 thỏa mãn 0a1,....a9CM...
Đọc tiếp
Bài 1:Cho a,b,c thuộc Q thỏa mãn abc=1
CMR: 1/ab+a+1+b/bc+b+1+1/abc+bc+b=1
Bài 2:a)1/2+1/3+2/3+1/4+2/4+3/4+...+1/n+2/n+...+n-/n(với n thuộc Z n>=2)
b)1/2-1/3-2/3+1/4+2/4+3/4-...-1/2k+1-2/2k+1-...-2k/2k+1(k thuộc N,k>=1)
c)1/2-1/3-2/3+1/4+2/4+3/4-...+1/2k+2/2k+...+2k-1/2k(k thuộc N , k>=1)
Bài 3:a)CMr 1/n-1/n+1=1/n(n+1) (với n thuộc N*)
b)1/n(n+1)-1/(n+1)(n+2)=2/n(n+1)(n+2)
c)-1-1/3-1/6-1/10-1/15-1/21-1/28-1/36-1/45
d)1/1.2.3+1/2.3.4+1/3.4.5+...+1/18.19.20
Bài 4:Cho các số hữu tỉ a1,a2,.....a9 thỏa mãn 0<a1,....<a9
CMR:a1+....+a9/a3+a6+a9<3
Làm giúp mk nhanh nha!!!..Mk đag cần gấp lmk
Đúng mk sẽ tick.Cảm ơn mn nhiều
Thanks...Arigato....
Cho p là số nguyên tố lẻ. Chứng minh rằng với mọi \(k\in N\), ta luôn có:
\(S=1^{2k+1}+2^{2k+1}+...+\left(p-1\right)^{2k+1}\) chia hết cho p
tại sao:(n+1)(n-1)(n+3) = (2k+4)(2k+2) (2k với n = 2k,k\(\in\)N)
Đề sai rồi:
Thay n=2k vào pt trên ta đc:
(n+1)(n-1)(n+3)=(n+4)(n+2)(n+3)
=>(n+1)(n-1)=(n+4)(n+2) (sai rồi)
Đúng 0
Bình luận (0)
các bạn có ai học sách toán đại hình nâng cao ko ??tiện thể giúp tớ 2 bài này nha. BÀI 1: cho hai đoạn A[a;a+2] và B[b;b+1]các số a,b cần thỏa mãn điều kiện gì để A giao B rỗng (cái này viết bằng kí hiệu)BÀI 2: choAleft{nin Zbackslash n2k,kin Zright}B là tập hợp các số nguyên có chữ số tận cùng là 0,2,4,6,8Cleft{nin Zbackslash n2k-2,kin Zright}Dleft{nin Zbackslash n3k+1,kin Zright}chứng minh rằng AB , AC , A neB
Đọc tiếp
các bạn có ai học sách toán đại hình nâng cao ko ??
tiện thể giúp tớ 2 bài này nha.
BÀI 1: cho hai đoạn A=[a;a+2] và B=[b;b+1]
các số a,b cần thỏa mãn điều kiện gì để "A giao B = rỗng'' (cái này viết bằng kí hiệu)
BÀI 2: cho
\(A=\left\{n\in Z\backslash n=2k,k\in Z\right\}\)
B là tập hợp các số nguyên có chữ số tận cùng là 0,2,4,6,8
\(C=\left\{n\in Z\backslash n=2k-2,k\in Z\right\}\)
\(D=\left\{n\in Z\backslash n=3k+1,k\in Z\right\}\)
chứng minh rằng A=B , A=C , A \(\ne\)B
cho a^2k+b^2k/c^2k+d^2k =a^2k-b^2k/c^2k-d^2k (k thuộc N )
Chứng minh a/b = +_ c/d
Cho 10^k-1chia hết cho 19 .CMR:a) 10^2k -1 chi hết 19
\(10^{2k}-1=\left(10^k-1\right)\left(10^k+1\right)⋮19\)
Đúng 2
Bình luận (0)
Rút gọn đa thức sau: (làm chi tiết hộ mình nhé)
\(\left(A+B\right)\left(A^{2k}-A^{2k-1}B+...+A^2B^{2k-2}-AB^{2k-1}+B^{2k}\right)\)
câu này là hằng đẳng thức thôi . nhưng nếu muốn làm chi tiết thì đây nha :))
ta có : \(\left(A+B\right)\left(A^{2K}-A^{2k-1}B+...+A^2.B^{2k-2}-AB^{2k-1}+B^{2k}\right)\)
\(=\left(A+B\right)\left(A^{2K}+B^{2k}-A^{2k-1}B+...+A^2.B^{2k-2}-AB^{2k-1}\right)\)
\(=A\left(A^{2k}+B^{2k}\right)+B\left(A^{2k}+B^{2k}\right)+A\left(-A^{2k-1}B+...+A^2B^{2k-2}-AB^{2k-1}\right)+B\left(A^{2k-1}B+...+A^2B^{2k-2}-AB^{2k-1}\right)\)
\(=A\left(A^{2k}+B^{2k}\right)+B\left(A^{2k}+B^{2k}\right)-A^{2k}B-B^{2k}A\)
\(=A^{2k+1}+AB^{2K}+BA^{2k}+B^{2k+1}-A^{2k}B-B^{2k}A\)
\(=A^{2k+1}+B^{2k+1}\)
Đúng 0
Bình luận (1)
Cho a và b là 2 số tự nhiên liên tiếp (ab). Chứng minh a và b nguyên tố cùng nhau. Giải:Vì a và b là 2 số tự nhiên liên tiếp a.b chia hết cho 2 Vì ba a có dạng 2k, b có dạng 2k+1 (k thuộc N*) a.b có dạng 2k.(2k+1)Gọi ƯCLN(2k;2k+1) d (d thuộc N*) 2k chia hết cho d ; 2k+1 chia hết cho d (2k+1)-2k chia hết cho d 2k+1-2k chia hết cho d 1 chia hết cho d d1 ƯCLN(a;b)1 a và b là 2 số nguyên tố cùng nhau.Mình giải như vây có đúng không?
Đọc tiếp
Cho a và b là 2 số tự nhiên liên tiếp (a<b). Chứng minh a và b nguyên tố cùng nhau.
Giải:
Vì a và b là 2 số tự nhiên liên tiếp
=> a.b chia hết cho 2
Vì b>a => a có dạng 2k, b có dạng 2k+1 (k thuộc N*)
=> a.b có dạng 2k.(2k+1)
Gọi ƯCLN(2k;2k+1) = d (d thuộc N*)
=> 2k chia hết cho d ; 2k+1 chia hết cho d
=> (2k+1)-2k chia hết cho d
=> 2k+1-2k chia hết cho d
=> 1 chia hết cho d
=> d=1
=> ƯCLN(a;b)=1
=> a và b là 2 số nguyên tố cùng nhau.
Mình giải như vây có đúng không?
theo mình thế này mới đúng
Vì a < b và a và b là 2 số tự nhiên liên tiếp => b = a + 1
Gọi ƯCLN(a,b) = d
=> \(\begin{cases}a⋮d\\b⋮d\end{cases}=>\orbr{\begin{cases}a⋮d\\a+1⋮d\end{cases}}\)
=> \(a+1-a⋮d=>1⋮d\)
=> \(d\inƯ\left(1\right)=>d=1\)
Vì (a,b) = 1 => a và b là 2 số nguyên tố cùng nhau
Đúng 0
Bình luận (0)
Nếu a<b thì b=a+1 rồi làm tượng tự từ chỗ " Gọi....." thôi. Ko cần phải dài dòng như vậy đâu, bài này mk làm nhiều rồi
Đúng 0
Bình luận (0)
nhưng mình hỏi là đúng hay sai mà chứ không bảo các bạn làm cách khác
Đúng 0
Bình luận (0)