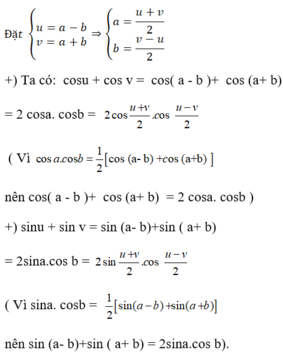Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được.

Những câu hỏi liên quan
Sử dụng công thức biến đổi tích thành tổng và đặt \(a + b = u;\,\,a - b = v\) biến đổi các biểu thức sau thành tích: \(\cos u + \cos v;\,\,\cos u - \cos v;\,\,\sin u + \sin v;\,\,\sin u - \sin v\)
\(\begin{array}{l}1.\,\,\,\,\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right] \Leftrightarrow 2\cos a.\cos b = \cos \left( {a + b} \right) + \cos \left( {a - b} \right)\\ \Leftrightarrow 2\cos \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \cos u + \cos v\\2.\,\,\,\,\sin a.\sin b = - \frac{1}{2}.\left[ {\cos \left( {a + b} \right) - \cos \left( {a - b} \right)} \right] \Leftrightarrow - 2.\sin a.\sin b = \cos \left( {a + b} \right) - \cos \left( {a - b} \right)\\ \Leftrightarrow - 2.\sin \frac{{u + v}}{2}.\sin \frac{{u - v}}{2} = \cos u - \cos v\\3.\,\,\,\,\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right] \Leftrightarrow 2\sin a.\cos b = \sin \left( {a + b} \right) + \sin \left( {a - b} \right)\\ \Leftrightarrow 2\sin \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \sin u + \sin v\\4.\,\,\,\,\sin \left( {a + b} \right) - \sin \left( {a - b} \right) = \sin a.\cos b + \cos a.\sin b - \sin a.\cos b + \cos a.\sin b = 2\cos a.\sin b\\ \Leftrightarrow \sin u - \sin v = 2.\cos \frac{{u + v}}{2}.\sin \frac{{u - v}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
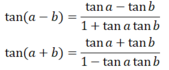
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
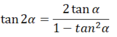
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
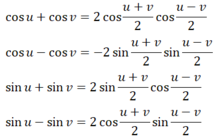
Đúng 0
Bình luận (0)
dùng công thức biến đổi tổng thành tích , giải các phương trình sau : a) \(\cos3x=\sin2x\) ; b) \(\sin\left(x-120^o\right)-\cos2x=0\)
dùng công thức biến đổi tổng thành tích , giải các phương trình sau : a) \(\cos3x=\sin2x\) ; b) \(\sin\left(x-120^o\right)-\cos2x=0\)
cos3x=sin(\(\dfrac{\pi}{2}\)-3x)
\(\Leftrightarrow\)sin(\(\dfrac{\pi}{2}\)-3x)=sin2x
\(\Leftrightarrow\)2x=\(\dfrac{\pi}{2}\)-3x+k2\(\pi\) or 2x=3x-\(\dfrac{\pi}{2}\)+k2\(\pi\)
\(\Leftrightarrow\)x=...
Đúng 0
Bình luận (0)
dùng công thức biến đổi tổng thành tích , giải các phương trình sau : a) \(\cos3x=\sin2x\) ; b) \(\sin\left(x-120^o\right)-\cos2x=0\)
): Em hãy biến đổi các công thức toán học sau sang công thức sẽ cài đặt trong Excel:
a/ 200 : 10 + 2 c/ (10+3).(2.10 -1)
b/ 64- 62.5 d/ [(45 - 7)*4]:2
a/=200/10+2
b/=6^4-6^2*5
c/=(10+3)*(2*10-1)
d/=[(45-7)*4]/2
Đúng 4
Bình luận (2)
a. 200/10+2
b. (10+3)*(2*10-1)
c. 6^4-6^2*5
d. [(45-7)*4]/2
Đúng 2
Bình luận (2)
Em hãy biến đổi các công thức toán học sáng công thức sẽ cài đặt trong Excel
Tham khảo!
Chúng ta sẽ lấy ví dụ về một công thức đơn giản.
1.Trên trang tính, hãy bấm vào ô mà bạn muốn nhập công thức vào đó.
2.Nhập = (dấu bằng) trước các hằng số và toán tử (tối đa lên đến 8192 ký tự) mà bạn muốn sử dụng trong phép tính.
Ví dụ: nhập =1+1.
3.Nhấn Enter (Windows) hoặc Return (máy Mac).
Chúng ta hãy lấy một biến thể khác của một công thức đơn giản. Nhập =5+2*3 vào một ô khác, rồi nhấn Enter hoặc Return. Excel nhân hai số cuối rồi cộng với số thứ nhất thành kết quả.
Đúng 0
Bình luận (0)
Bằng cách đặt u = a – b, v = a + b, hãy biến đổi cosu + cosv, sinu + sinv thành tích.
Cho tích phân
I
∫
0
1
2
x
+
1
2
d
x
1. Tính I bằng cách khai triển
2
x
+
1
2
.2. Đặt u 2x + 1. Biến đổi biểu thức ...
Đọc tiếp
Cho tích phân I = ∫ 0 1 2 x + 1 2 d x
1. Tính I bằng cách khai triển 2 x + 1 2 .
2. Đặt u = 2x + 1. Biến đổi biểu thức 2 x + 1 2 dx thành g(u)du.
3. Tính ∫ u 0 u 1 g u d u và so sánh kết quả với I trong câu 1
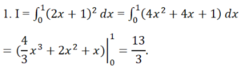
2. Vì u = 2x+1 nên du = 2dx. Ta có 2 x + 1 2 d x = u 2 d u 2

Đúng 0
Bình luận (0)