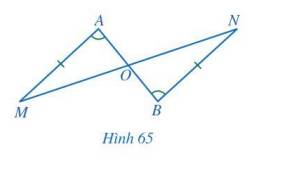
Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON.
Cho biết A\(\widehat{O}\)B =120o. trong góc AOB vẽ các tia OM và ON sao cho OA⊥OM, OB⊥ON
a) Tính số đo các gọc: AOM,BON.
b) Chứng minh : N\(\widehat{O}\)A=M\(\widehat{O}\)B
a) Ta có: OA ⊥ OM (GT)
\(\Rightarrow\widehat{AOM}=90^0\)
Ta có: OB ⊥ ON (GT)
\(\Rightarrow\widehat{BON}=90^0\)
b)
Ta có: \(\left\{{}\begin{matrix}\widehat{AON}+\widehat{NOM}=90^0\left(=\widehat{AOM}\right)\\\widehat{BOM}+\widehat{NOM}=90^0\left(=\widehat{BON}\right)\end{matrix}\right.\)
=> Góc AON = Góc BOM
Cho góc \(xOy\). Trên tia Ox lấy các điểm A, B sao cho \(OA = 2cm,\,\,OB = 9cm\). Trên tia Oy lấy các điểm M, N sao cho \(OM = 3cm,\,\,ON = 6cm\). ChỨNG minh \(\widehat {OBM} = \widehat {ONA}\).
Ta thấy
\(\begin{array}{l}\frac{{OA}}{{OM}} = \frac{2}{3};\,\,\frac{{ON}}{{OB}} = \frac{6}{9} = \frac{2}{3}\\ \Rightarrow \frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\end{array}\)
Xét tam giác OAN và tam giác OMB có:
\(\frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\) và \(\widehat O\) chung
\( \Rightarrow \Delta OAN \backsim \Delta OMB\) (c-g-c)
\( \Rightarrow \widehat {OBM} = \widehat {ONA}\)
Cho \(\widehat{xOy}\)= 120 độ. Vẽ bên trong góc xOy hai tia Oa, Ob sao cho Oa vuông góc với Oy, Ob vuông góc với Ox. Vẽ tia Om là tia phân giác của \(\widehat{aOb}\).
a) Chứng minh Om là tia phân giác của góc xOy.
b) Vẽ tia On sao cho tia Ox là tia phân giác của góc mOn. Chứng minh Oa vuông góc với On, từ đó suy ra hai tia On và Oy cùng chung một đường thẳng
MÌNH CẦN GẤP NHÉ, AI LÀM XONG MÌNH SẼ TICK
KO CẦN HÌNH VẼ CŨNG ĐC NHÉ
a ) Vì Oa ⊥⊥ OM
=> aOmˆaOm^ = 90o
Mà MOaˆMOa^ + aONˆaON^ = MONˆMON^
=> aOnˆaOn^ = MONˆMON^ - MOaˆMOa^ = 120o - 90o = 30o
Vậy aONˆaON^ = 30o
Vì Ob ⊥⊥ ON
=> bONˆbON^ = 90o
Mà bOMˆbOM^ + bONˆbON^ = MONˆMON^
=> bOMˆbOM^= MONˆMON^ - bONˆbON^ = 120o - 90o = 30o
Vậy bOMˆbOM^ = aONˆ
Cho góc \(\widehat{AOB}=100^o\). Vẽ 2 tia OM và ON nằm trong góc \(\widehat{AOB}\)sao cho OM \(\perp\)OA và ON \(\perp\)OB
a) Tính số đo \(\widehat{MON}\)
b) Gọi Oa và Ob lần lượt là hai tia phân giác của hai góc \(\widehat{AON}\)và \(\widehat{BOM}\). Chứng tỏ rằng Oa \(\perp\)Ob
a) Ta có :
AOM + BON = 180độ
hay AON + MON + BOM + MON = 180
AON + BOM + 2MON = 180
mà AON + MON + BOM = AOB = 100độ
=> MON + 100 = 180
=> MON = 80độ
Tự vẽ hình nhau Đ
a) Ta có: \(\widehat{AOM}+\widehat{NOB}=90^0+90^0=180^0\)
Mà \(\widehat{AOM}=\widehat{AON}+\widehat{MON}\)
\(\widehat{NOB}=\widehat{MON}+\widehat{MOB}\)
\(\Rightarrow\widehat{AON}+\widehat{MON}+\widehat{MON}+\widehat{MOB}=180^0\)
Mà \(\widehat{AON}+\widehat{MON}+\widehat{MOB}=100^0=\widehat{AOB}\)
\(\Rightarrow\widehat{AON}+2\widehat{MON}+\widehat{MOB}=100^0+\widehat{MON}=180^0\)
\(\Rightarrow\widehat{MON}=180^0-100^0=80^0\)
b) \(\widehat{AON}=90^0-\widehat{MON}=90^0-80^0=10^0\)
Mà Oa là tia phân giác của góc AON \(\Rightarrow\widehat{AOa}=\widehat{NOa}=\frac{\widehat{AON}}{2}=\frac{10^0}{2}=5^0\)
\(\widehat{MOB}=90^0-\widehat{MON}=90^0-80^0=10^0\)
Mà Ob là tia phân giác của góc BOM \(\Rightarrow\widehat{MOb}=\widehat{Bob}=\frac{\widehat{BOM}}{2}=\frac{10^0}{2}=5^0\)
\(\Rightarrow\widehat{aOb}=\widehat{NOa}+\widehat{MON}+\widehat{MOb}=80^0+5^0+5^0=90^0\)
Vậy \(Oa\perp Ob\)
Cho hình chóp O.ABC có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \). Chứng minh rằng:
a) \(BC \bot OA\)
b) \(CA \bot OB\)
c) \(AB \bot OC\)
a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
1, Cho \(\widehat{MON}=\) 1200 . Vẽ các tia Oa , Ob trong góc đó sao cho Oa vuông góc với OM , Ob vuông góc với ON.
a, chứng tỏ \(\widehat{aON}=\widehat{bOM}\)
b, Vẽ tia \(Ox;Oy\)là các tia phân giác của các góc \(\widehat{aON;}\widehat{bOM}\). Chứng tỏ \(Ox\)vuông góc với \(Oy\)
c, Kể tên những cặp góc có cạnh tương ứng vuông góc
Nhờ mọi người vẽ hình và giúp mk nha. THANKS NHÌU
Bài 2: (Vẽ hình) Cho \(\widehat{xOy}\). Trên tia \(Ox\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA=OB\). Gọi \(C\) là 1 điểm trên tia phân giác \(Oz\) của \(\widehat{xOy}\). Chứng minh rằng:
a, \(AC=BC\)
\(\widehat{xAC}=\widehat{yBC}\)
b, \(OC=OB\)
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
Cho tam giác ABC , O nằm trong tam giác đó. Các tia AO,BO,CO cắt BC,CA,AB tại M,N,P. Chứng minh rằng:
\(\sqrt{\frac{OA}{OM}}+\sqrt{\frac{OB}{ON}}+\sqrt{\frac{OC}{OP}}\ge3\sqrt{2}\)
\(\sqrt{\frac{AM}{OA}}+\sqrt{\frac{BN}{OB}}+\sqrt{\frac{CP}{OC}}\ge\frac{3\sqrt{6}}{2}\)
\(\sqrt{\frac{OM}{AM}}+\sqrt{\frac{ON}{BN}}+\sqrt{\frac{OP}{CP}}\ge\sqrt{3}\)
Đã chứng minh:
\(\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}\ge9\)
\(\frac{OA}{AM}+\frac{OB}{ON}+\frac{OC}{OP}\ge6\)
\(\frac{AM}{OA}+\frac{BN}{OB}+\frac{CP}{OC}\ge\frac{9}{2}\)
\(\frac{OM}{OA}+\frac{ON}{OB}+\frac{OP}{OC}\ge\frac{3}{2}\)
( bài toán cực trị trong hình học).
a. Đặt \(S_{AOB}=c^2;S_{BOC}=a^2;S_{COA}=b^2\Rightarrow S_{ABC}=a^2+b^2+c^2\)
Ta có \(\frac{AM}{OM}=\frac{S_{ABC}}{S_{BOC}}=\frac{a^2+b^2+c^2}{a^2}=1+\frac{b^2+c^2}{a^2}\)
Vậy thì \(\frac{OA}{OM}=\frac{AM}{OM}-1=\frac{b^2+c^2}{a^2}\Rightarrow\sqrt{\frac{OA}{OM}}=\sqrt{\frac{b^2+c^2}{a^2}}\ge\frac{1}{\sqrt{2}}\left(\frac{b}{a}+\frac{a}{b}\right)\)
Tương tự, ta có: \(\sqrt{\frac{OA}{OM}}+\sqrt{\frac{OB}{ON}}+\sqrt{\frac{OC}{OP}}\ge\frac{1}{\sqrt{2}}\left(\frac{a}{b}+\frac{c}{b}+\frac{a}{c}+\frac{b}{c}+\frac{b}{a}+\frac{c}{a}\right)\ge\frac{1}{\sqrt{2}}.6=3\sqrt{2}\)
Cho \(\widehat{xOy}\)vuông có Oz là tia phân giác. Trên tia Oz lấy điểm M tùy ý \(\left(M\ne O\right)\)Gọi A và B lần lượt là hình chiếu của M trên tia Ox và Oy.
a) Chứng minh: OA = OB.
b) Trên đoạn thẳng AM lấy điểm I, trên đoạn MB lấy điểm K sao cho \(\widehat{AIO}=\widehat{KIO}.\)Chứng minh: \(\widehat{AOI}=\widehat{HOI}\)(với H là hình chiếu của điểm O trên đường thẳng IK)
c) Tính \(\widehat{IOK}.\)
Giúp mình với !!!!!
Nếu đề bài đúng thì làm hộ mình, còn nếu đề bài sai thì các bn sửa lại và làm giúp mình nha! *-*