tam giác ABC có A=\(75^o\), B=\(45^o\), AC=2. tính cạnh AB.

Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat B = {75^o},\widehat C = {45^o}\) và BC = 50. Tính độ dài cạnh AB.
Ta có: \(\widehat B = {75^o},\widehat C = {45^o}\)\( \Rightarrow \widehat A = {180^o} - \left( {{{75}^o} + {{45}^o}} \right) = {60^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin {45^o}.\frac{{50}}{{\sin {{60}^o}}} \approx 40,8\)
Vậy độ dài cạnh AB là 40,8.
Đúng 1
Bình luận (0)
Cho tam giác ABC có \(\stackrel\frown{B}\) = \(75^o\), \(\stackrel\frown{C}=45^o\) và BC = 50.
a) Tính độ dài cạnh AB.
b) Tính diện tích tam giác ABC.
c) Tính đường cao xuất phát từ đỉnh A của tam giác ABC
a: Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-75^0-45^0=60^0\)
Xét ΔABC có
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
=>\(\dfrac{AB}{sin45}=\dfrac{50}{sin60}\)
=>\(AB\simeq40,82\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot40,82\cdot50\cdot sin75\simeq985,73\)
c: Độ dài đường cao xuất phát từ A là:
\(2\cdot\dfrac{985.73}{50}=39,4292\left(\right)\)
Đúng 1
Bình luận (0)
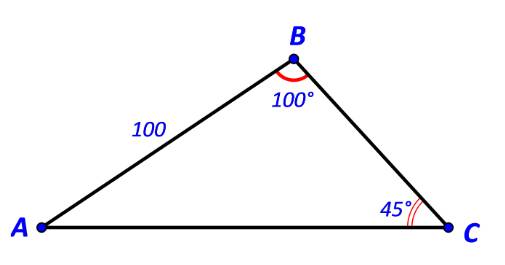
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat A = {45^o}\). Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Áp dụng định lí cosin trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\end{array}\)
(trong đó: AB = c, BC = a và AC = b)
Ta được: \(B{C^2} = {a^2} = {8^2} + {5^2} - 2.8.5.\cos {45^o} = 89 - 40\sqrt 2 \)\( \Rightarrow BC \approx 5,7\)
Từ (2) suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\);
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
\( \Rightarrow \cos B \approx \frac{{ - 217}}{{1900}} \Rightarrow \widehat B \approx {97^o} \Rightarrow \widehat C \approx {38^o}\)
Vậy tam giác ABC có BC = 5,7, \(\widehat B = {97^o},\widehat C = {38^o}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A=75 , C=45 và AC=a\(\sqrt{2}\) . Vẽ đường cao AK
a, Tính AB , KC theo a
b, Gọi H là trực tâm của tam giác ABC và O là tâm đường tròn ngoại tiếp tam giác ABC . Tính OHC
c, Gọi I là tâm đt nội tiếp tam giác ABC . Tính bán kính đt ngoại tiếp tam giác HOT theo a
Cho tam giác ABC có A=45o; B=75o. Ta có:
A. AB<BC<CA B. BC<AB<AC C. CA<AB<BC D.CA<BC<AB
Cho tam giác ABC có A=45o; B=75o. Ta có:
B.BC<AB<AC
Hok tot
Đúng 0
Bình luận (0)
Cho tam giác ABC có A=45o; B=75o. Ta có:
A. AB<BC<CA B. BC<AB<AC C. CA<AB<BC D.CA<BC<AB
tam giác ABC có các góc A=75, B=45. tính tỉ số AB/AC
Áp dụng đl tổng 3 góc trong tam giác:
\(\Rightarrow\widehat{C}=180^o-75^o-45^o=60^o\)
Ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\\ \Rightarrow\dfrac{AB}{AC}=\dfrac{sinC}{sinB}=\dfrac{\sqrt{6}}{2}\)
$HaNa$
Đúng 3
Bình luận (0)
Mà: \(\widehat{C}=180^o-75^o-45^o=60^o\)
Ta có:
\(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{sinC}{sinB}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{sin60^o}{sin45^o}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{\sqrt{2}}{2}}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{\sqrt{2}}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{2}\)
Đúng 2
Bình luận (0)
Tam giác ABC có B = 60 o ; C = 45 o ; BC = a a)Tính độ dài các cạnh AB, AC














