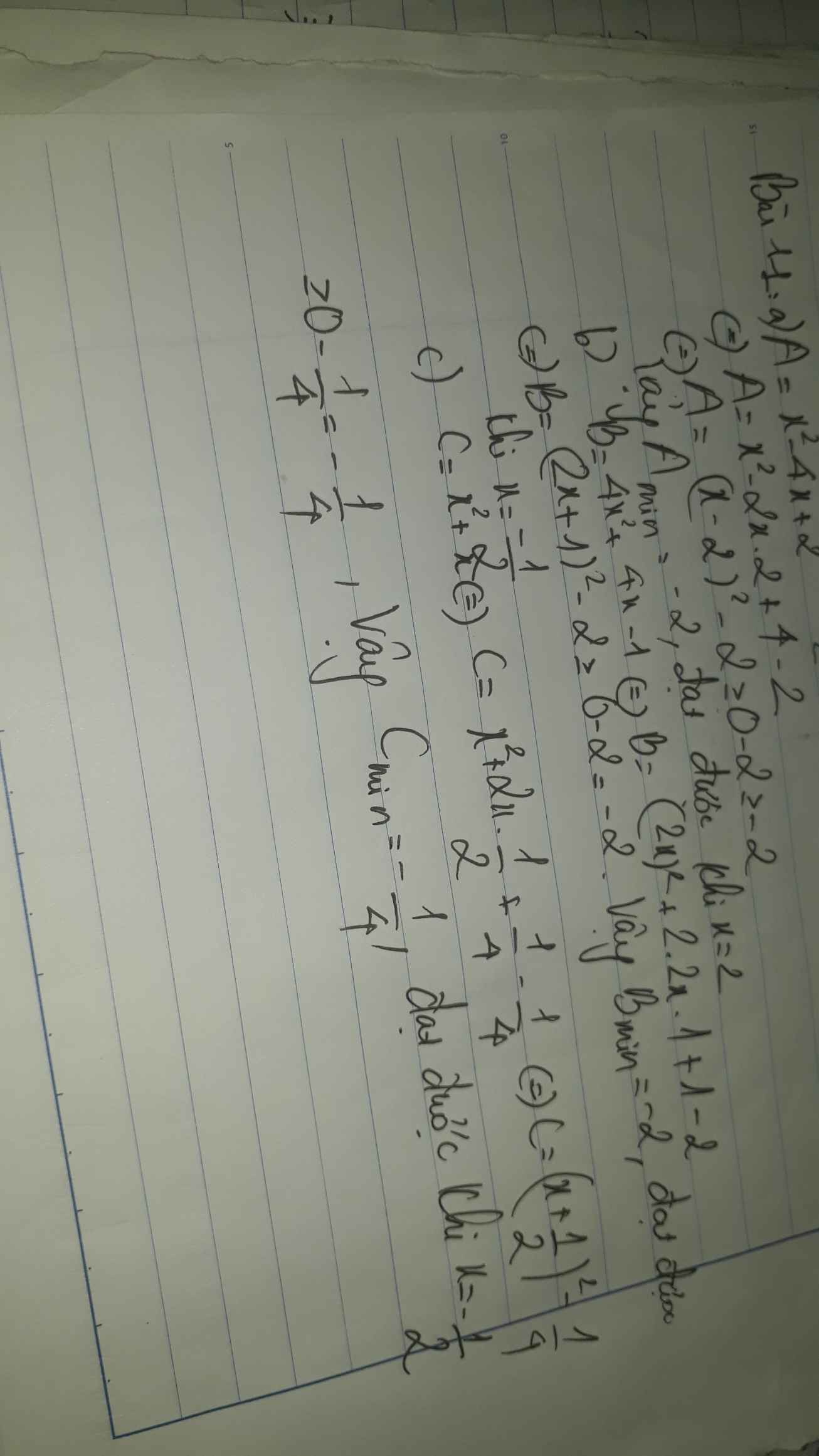a và b chắc của lớp 9 nhỉ

\(x^2-2x+2=x^2-x-x+2\)

\(=x\left(x-1\right)-\left(x-1\right)+1\)

\(=\left(x-1\right)^2+1\)

\(9x^2-6x+5=9\left(x^2-\frac{2}{3}x+\frac{5}{9}\right)\)

\(=9\left(x^2-\frac{1}{3}x-\frac{1}{3}x+\frac{5}{9}\right)\)

\(=9\left(x^2-\frac{1}{3}x-\frac{1}{3}x+\frac{1}{9}+\frac{4}{9}\right)\)

\(=9\left[x\left(x-\frac{1}{3}\right)-\frac{1}{3}\left(x-\frac{1}{3}\right)+\frac{4}{9}\right]\)

\(=9\left[\left(x-\frac{1}{3}\right)^2+\frac{4}{9}\right]\)

\(=9\left(x-\frac{1}{3}\right)^2+4\)

Cái kia tương tự.

c)x²-2x+2

=x²-2x+1+1

=(x-1)²+1

=(x-1)²-i²

^{=[(x-1)-i][(x-1)+i}

=(x-1-i)(x-1+i)

b)9x²-6x+5

=9x²-3x-3x+5

=3x(3x-5)-5(3x-5)

=(3x-1)²

c)30-20x+4x²

^{chịu ,khó was ! k lm dc !!!!!!!!!!!!!!!!!!}

Bài 1: 

a) Ta có: \(A=-x^2-4x-2\)

\(=-\left(x^2+4x+2\right)\)

\(=-\left(x^2+4x+4-2\right)\)

\(=-\left(x+2\right)^2+2\le2\forall x\)

Dấu '=' xảy ra khi x=-2

b) Ta có: \(B=-2x^2-3x+5\)

\(=-2\left(x^2+\dfrac{3}{2}x-\dfrac{5}{2}\right)\)

\(=-2\left(x^2+2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{49}{16}\right)\)

\(=-2\left(x+\dfrac{3}{4}\right)^2+\dfrac{49}{8}\le\dfrac{49}{8}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{3}{4}\)

c) Ta có: \(C=\left(2-x\right)\left(x+4\right)\)

\(=2x+8-x^2-4x\)

\(=-x^2-2x+8\)

\(=-\left(x^2+2x-8\right)\)

\(=-\left(x^2+2x+1-9\right)\)

\(=-\left(x+1\right)^2+9\le9\forall x\)

Dấu '=' xảy ra khi x=-1

Bài 2: 
a) Ta có: \(=25x^2-20x+7\)

\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)

\(=\left(5x-2\right)^2+3>0\forall x\)

b) Ta có: \(B=9x^2-6xy+2y^2+1\)

\(=9x^2-6xy+y^2+y^2+1\)

\(=\left(3x-y\right)^2+y^2+1>0\forall x,y\)

c) Ta có: \(E=x^2-2x+y^2-4y+6\)

\(=x^2-2x+1+y^2-4y+4+1\)

\(=\left(x-1\right)^2+\left(y-2\right)^2+1>0\forall x,y\)

chuyển vế sang r phân tích thành nhân tử, có thể dùng máy tính bỏ túi nhé bạn

câu 1: 9\(x^2\) + 12\(x\) + 5  =11

           (3\(x\))² + 2.3.\(x\) .2 + 2² + 1 = 11

           (3\(x\) + 2)²      =  11 - 1

             (3\(x\) + 2)²    = 10

               \(\left[{}\begin{matrix}3x+2=\sqrt{10}\\3x+2=-\sqrt{10}\end{matrix}\right.\)

                \(\left[{}\begin{matrix}3x=\sqrt{10}-2\\3x=-\sqrt{10}-2\end{matrix}\right.\)

                  \(\left[{}\begin{matrix}x=\dfrac{\sqrt{10}-2}{3}\\x=\dfrac{-\sqrt{10}-2}{3}\end{matrix}\right.\)

                 Vậy S = {\(\dfrac{-\sqrt{10}-2}{3}\); \(\dfrac{\sqrt{10}-2}{3}\)} 

  Câu 2: 6\(x^2\) + 16\(x\) + 12 = 2\(x^2\)

              6\(x^2\) + 16\(x\) + 12 - 2\(x^2\) = 0

              4\(x^2\) + 16\(x\) + 12 = 0

              (2\(x\))² + 2.2.\(x\).4 + 16 - 4 = 0

               (2\(x\) + 4)²   = 4

               \(\left[{}\begin{matrix}2x+4=2\\2x+4=-2\end{matrix}\right.\) 

                \(\left[{}\begin{matrix}2x=-2\\2x=-6\end{matrix}\right.\)

                 \(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)

              S = { -3; -1}

3, 16\(x^2\) + 22\(x\) + 11 = 6\(x\) + 5

    16\(x^2\) + 22\(x\) - 6\(x\)  + 11 - 5 = 0

     16\(x^2\) + 16\(x\) + 6 = 0

      (4\(x\))² + 2.4.\(x\) . 2 + 2² + 2 = 0

       (4\(x\) + 2)² + 2 = 0 (1) 

Vì (4\(x\)+ 2)² ≥ 0 ∀ ⇒ (4\(x\) + 2)² + 2 > 0 ∀ \(x\) vậy (1) Vô nghiệm

             S = \(\varnothing\)

Câu 4. 12\(x^2\) + 20\(x\) + 10 = 3\(x^2\) - 4\(x\) 

            12\(x^2\) + 20\(x\) + 10 - 3\(x^2\) + 4\(x\) = 0

            9\(x^2\) + 24\(x\) + 10 = 0

           (3\(x\))² + 2.3.\(x\).4 + 16 - 6 = 0

          (3\(x\) + 4)² = 6

            \(\left[{}\begin{matrix}3x+4=\sqrt{6}\\3x+4=-\sqrt{6}\end{matrix}\right.\)

              \(\left[{}\begin{matrix}3x=-4+\sqrt{6}\\3x=-4-\sqrt{6}\end{matrix}\right.\)

              \(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}-4}{3}\\x=-\dfrac{\sqrt{6}+4}{3}\end{matrix}\right.\)

                    S = {\(\dfrac{-\sqrt{6}-4}{3}\); \(\dfrac{\sqrt{6}-4}{3}\)}

Bài 4

c) x(x - 2) + (x - 2)²

= (x - 2)(x + x - 2)

= (x - 2)(2x - 2)

= 2(x - 2)(x - 1)

d) 2x(x - y)² - 5(y - x)

= 2x(x - y)² + 5(x - y)

= (x - y)(2x + 5)

Bài 5

a) x² - 6x - 2xy + 12y

= (x² - 6x) - (2xy - 12y)

= x(x - 6) - y(x - 6)

= (x - 6)(x - y)

b) 10ax - 5ay - 2x + y

= (10ax - 5ay) - (2x - y)

= 5a(2x - y) - (2x - y)

= (2x - y)(5a - 1)

c) x⁴ + x³y - x - y

= (x⁴ + x³y) - (x + y)

= x³(x + y) - (x + y)

= (x + y)(x³ - 1)

= (x + y)(x - 1)(x² + x + 1)

d) x³ + 2x² - 4x - 8

= (x³ + 2x²) - (4x + 8)

= x²(x + 2) - 4(x + 2)

= (x + 2)(x² - 4)

= (x + 2)(x + 2)(x - 2)

= (x + 2)²(x - 2)

e) xy - 5x - y² + 5y

= (xy - 5x) - (y² - 5y)

= x(y - 5) - y(y - 5)

= (y - 5)(x - y)

f) ax - bx - 2cx - 2a + 2b + 4c

= (ax - bx - 2cx) - (2a - 2b - 4c)

= x(a - b - 2c) - 2(a - b - 2c)

= (a - b - 2c)(x - 2)

g) 5x²y + 5xy² - b²x - b²y

= (5x²y + 5xy²) - (b²x + b²y)

= 5xy(x + y) - b²(x + y)

= (x + y)(5xy - b²)

h) 4x³ - 4x² - 9x + 9

= (4x³ - 4x²) - (9x - 9)

= 4x²(x - 1) - 9(x - 1)

= (x - 1)(4x² - 9)

= (x - 1)(2x - 3)(2x + 3)

bạn xem lại đề bài 1 là GTNN hay GTLN nha

Giúp vs ạ mk đag cần

.

4x2 hay là 4x² vậy bạn ?