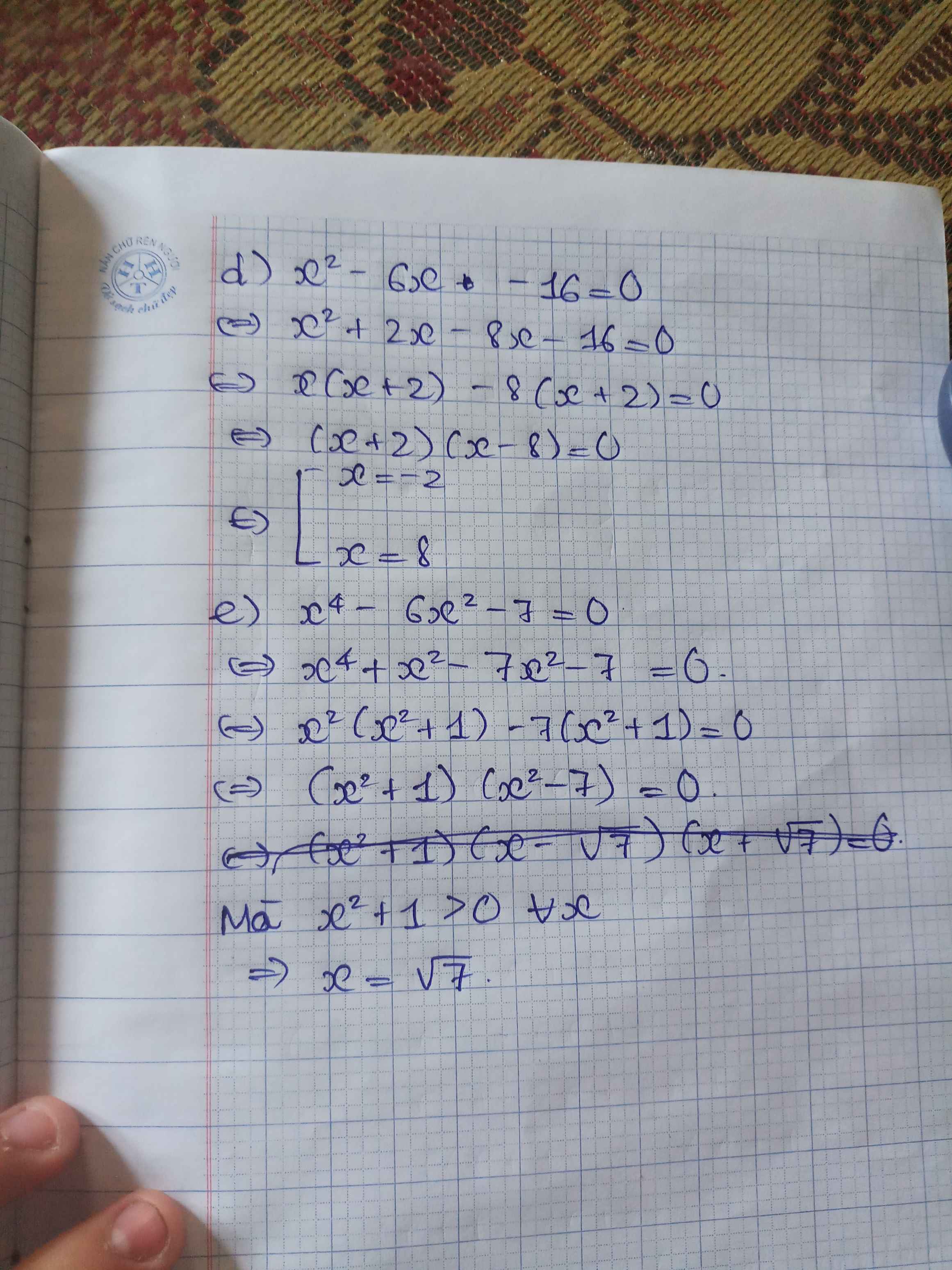Giải phương trình x6 + 6x4 - 36x3 + 6x2 + 1= 0.

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm
x
6
+
3
x
5
+
6
x
4
−
m
x
3
+
6
x
2
+
3
x
+
1
0
A. Vô số B. 26 C. 27 D. 28
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm x 6 + 3 x 5 + 6 x 4 − m x 3 + 6 x 2 + 3 x + 1 = 0
A. Vô số
B. 26
C. 27
D. 28
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm:
x 6 + 3 x 5 + 6 x 4 - m x 3 + 6 x 2 + 3 x + 1 = 0
A. Vô số
B. 26
C. 27
D. 28
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
Bảng biến thiên:
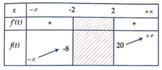
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
Đúng 0
Bình luận (0)
Không phải lớp 3 nhe nhầm lớp rùi
Tính giá trị của đa thức P(x)= x6-6x5+6x4-6x3+6x2-6x+1 tại x=5
\(P\left(x\right)=5^6-6.5^5+6.5^4-6.5^3+6.5^2-6.5+1=5^6-6\left(5^5-5^4-5^3-5^2-5\right)+1=1556\)
Đúng 0
Bình luận (0)
mình quên là k dùng máy tính bỏ túi nha
Đúng 0
Bình luận (0)
\(P\left(x\right)=x^6-6x^5+6x^4-6x^3+6x^2-6x+1\)
\(=x^6-5x^5-x^5+5x^4+x^4-5x^3-x^3+5x^2+x^2-5x-x+1\)
\(=x^5\left(x-5\right)-x^4\left(x-5\right)+x^3\left(x-5\right)-x^2\left(x-5\right)+x\left(x-5\right)-x+1\)
-Thay \(x=5\) vào P(x) ta được:
\(P\left(5\right)=5^5\left(5-5\right)-5^4\left(5-5\right)+5^3\left(5-5\right)-5^2\left(5-5\right)+5\left(5-5\right)-5+1\)\(=-5+1=-4\)
Đúng 1
Bình luận (0)
Tìm m để phương trình
x
6
+
6
x
4
-
m
3
x
3
+
(
15
-
3
m
2
)...
Đọc tiếp
Tìm m để phương trình x 6 + 6 x 4 - m 3 x 3 + ( 15 - 3 m 2 ) x 2 - 6 m x + 10 = 0 có đúng hai nghiệm phân biệt thuộc [1/2;2]
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm m để phương trình
x
6
+
6
x
4
-
m
3
x
3
+
15
-
3
m
2...
Đọc tiếp
Tìm m để phương trình x 6 + 6 x 4 - m 3 x 3 + 15 - 3 m 2 x 2 - 6 m x + 10 = 0 có đúng hai nghiệm phân biệt thuộc 1 2 ; 2
A. 11 5 < m < 4
B. 2 < m ≤ 5 2
C. 0 < m < 9 4
D. 7 5 ≤ m < 3
Chọn đáp án B
Phương trình đã cho tương đương với:
![]()
![]()
![]()
Xét hàm số f t = t 3 + 3 t trên ℝ
Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên ℝ
Suy ra
![]()
![]()
Xét hàm số g x = x + 1 x trên 1 2 ; 2
Ta có g ' x = 1 - 1 x 2
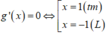
Bảng biến thiên:
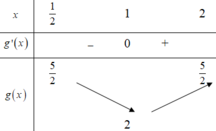
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên 1 2 ; 2
⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x tại hai điểm phân biệt trên 1 2 ; 2
⇔ 2 < m ≤ 5 2
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m để bất phương trình
x
6
+
6
x
4
+
15
-
3
m
2
x
2
-...
Đọc tiếp
Có bao nhiêu số nguyên m để bất phương trình x 6 + 6 x 4 + 15 - 3 m 2 x 2 - 6 m x + 10 ≥ 0 nghiệm đúng với mọi số thực x.
A. 4
B. 3
C. Vô số
D. 5
Chọn đáp án D.
Bất phương trình tương đương với
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
![]()
Có 5 số nguyên thoả mãn
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m để bất phương trình
x
6
+
6
x
4
-
m
3
x
3
+
15
-
3
m
2
x
2
-
6
m
x
+
10
≥
0
...
Đọc tiếp
Có bao nhiêu số nguyên m để bất phương trình x 6 + 6 x 4 - m 3 x 3 + 15 - 3 m 2 x 2 - 6 m x + 10 ≥ 0 nghiệm đúng với mọi số thực x.
A. 4
B. 3
C. Vô số
D. 5
Bất phương trình tương đương với:
![]()
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f ( t ) = t 3 + 3 t đồng biến trên R.
Vậy ![]()
![]()
Có 5 số nguyên thoả mãn.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Tập hợp tất cả các giá trị thực của tham số m để phương trình x6 +6x4 -m3x3 +(15 -3m2)x2 -6mx +10 =0 có đúng hai nghiệm phân biệt thuộc đoạn \(\left[\dfrac{1}{2};2\right]\) là?
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
Tìm x:
a) 36x3-4x=0
b) 3x(x-2)-2+x=0
c) (x3-x2)-4x2+8x-4=0
d) x2-6x-16=0
e) x4-6x2-7=0
(Mình cần gấp ạ)
a) Ta có: \(36x^3-4x=0\)
\(\Leftrightarrow4x\left(9x^2-1\right)=0\)
\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)
b) Ta có: \(3x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
d) Ta có: \(x^2-6x-16=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
e) Ta có: \(x^4-6x^2-7=0\)
\(\Leftrightarrow\left(x^2-7\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x\in\left\{\sqrt{7};-\sqrt{7}\right\}\)
Đúng 0
Bình luận (0)