Chọn \(A\).

Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.­­­­­­­mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

#include <bits/stdc++.h>

using namespace std;

long long i,n,x,k;

int main()

{

cin>>n>>k;

for (i=1; i<=n; i++)

{

cin>>x;

if (x==k) cout<<i<<" ";

}

return 0;

}

Tham khảo:

a. Viết chương trình phython thực hiện tìm kiếm tuần tự

def search(arr, n, x):

    for i in range (0, n):

        if (arr[i] == x):

            return i;

    return -1;

# Driver Code

arr = [ 2, 3, 4, 10, 40 ];

x = 10;

n = len(arr);

result = search(arr, n, x)

if(result == -1):

    print("Element is not present in array")

else:

    print("Element is present at index", result);

b. Viết phiên bản tìm kiếm tuần tự thứ hai, dùng vòng lặp for thay cho vòng lặp while (hoặc ngược lại).

def search(arr, n, x):

    for i in range (0, n):

        if (arr[i] == x):

            return i;

    return -1;

# Driver Code

arr = [ 2, 3, 4, 10, 40 ];

x = 10;

n = len(arr);

result = search(arr, n, x)

if(result == -1):

    print("Element is not present in array")

else:

    print("Element is present at index", result);

c. Viết phiên bản tìm kiếm tuần tự có thêm hai tham số đầu vào lo và hi tương tự như của hàm index. So sánh kết quả với phương thức index của phython.

def search(arr, n, x):

    for i in range (0, n):

        if (arr[i] == x):

            return i;

    return -1;

# Driver Code

arr = [ 2, 3, 4, 10, 40 ];

x = 10;

n = len(arr);

result = search(arr, n, x)

if(result == -1):

    print("Element is not present in array")

else:

    print("Element is present at index", result);

a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:

- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5

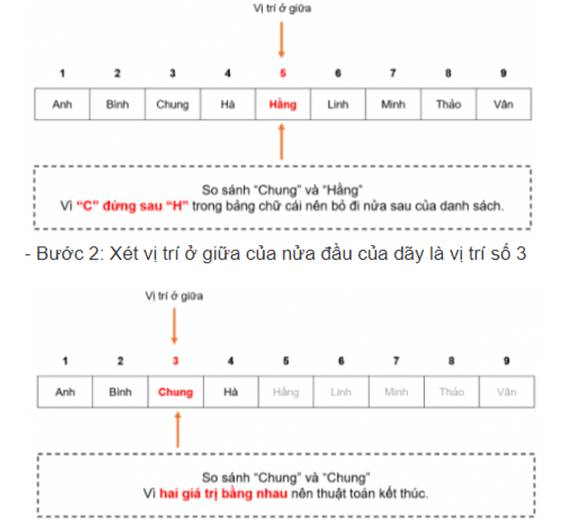
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.

b) Thuật toán tìm kiếm nhị phân

- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.

Thuật toán tuần tự

- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.

- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.

- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.

Để tìm phần tử có giá trị bằng 34 trong dãy A = {0, 4, 9, 10, 12, 14, 17, 18, 20, 31, 34, 67} bằng thuật toán tìm kiếm tuần tự, ta sẽ duyệt qua từng phần tử của dãy cho đến khi tìm thấy phần tử cần tìm.

Vì phần tử 34 nằm ở vị trí thứ 11 trong dãy, nên số lần duyệt cần thực hiện để tìm ra phần tử này là 11 lần, bao gồm cả phần tử 34.

Vậy, cần duyệt qua 11 phần tử để tìm ra phần tử có giá trị bằng 34 trong dãy A

Đáp án C

Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức  f ' x f x = 2 - 2 x *  

Lấy nguyên hàm 2 vế (*), ta được  ∫ d f x f x = ∫ 2 - 2 x d x

⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C  

Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó  f x = e - x 2 + 2 x  

Xét hàm số  f x = e - x 2 + 2 x  trên - ∞ ; + ∞ , có  f ' x = - 2 x + 2 = 0 ⇔ x = 1

Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0  

Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt  ⇔ 0 < m < e .

Đáp án là B.

Phương trình hoàng độ giao điểm của

C & d : x + m 2 x − 1 = − x + 1 ;   x ≠ 1 2  

⇔ 2 x 2 + 2 m x − m − 1 = 0  (1)

C & d  cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .

Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0    ⇔ m ∈ ℝ .

Xét phương trình hoành độ giao điểm:

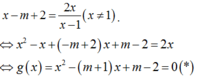
Để đường thẳng d cắt (C) tại 2 điểm phân biệt ⇔ p t *  có 2 nghiệm phân biệt khác 1.

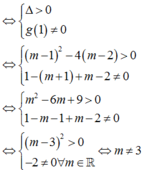
Gọi x A ;   x B  là 2 nghiệm phân biệt của (*), áp dụng định lí Vi-ét ta có: 

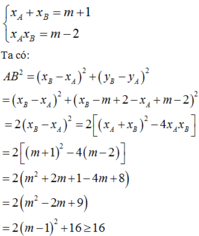
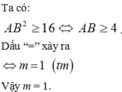
Chọn D.