y=x+m-1

=>x-y+m-1=0

Khoảng cách từ O(0;0) đến (d) là:

\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+m-1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\left|m-1\right|}{\sqrt{2}}\)

Để \(d\left(O;\left(d\right)\right)=3\sqrt{2}\) thì \(\dfrac{\left|m-1\right|}{\sqrt{2}}=3\sqrt{2}\)

=>|m-1|=6

=>\(\left[{}\begin{matrix}m-1=6\\m-1=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=7\\m=-5\end{matrix}\right.\)

Với \(m=-1\) thì d qua O nên k/c bằng 0 (loại), với \(m=2\) thì đường thẳng (d) có dạng \(y=3\) nên k/c từ O đến (d) bằng 3 (loại)

Với \(m\ne\left\{-1;2\right\}\)

Gọi A và B lần lượt là giao điểm của (d) với Ox và Oy

\(\Rightarrow x_A=-\dfrac{m+1}{m-2}\) ; \(y_B=m+1\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|x_A\right|=\left|\dfrac{m+1}{m-2}\right|\\OB=\left|y_B\right|=\left|m+1\right|\end{matrix}\right.\)

Gọi H là chân đường cao hạ từ O xuống d \(\Rightarrow OH\) là đường cao trong tam giác vuông OAB (vuông tại O) đồng thời \(OH=1\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\Leftrightarrow1=\left(\dfrac{m-2}{m+1}\right)^2+\dfrac{1}{\left(m+1\right)^2}\)

\(\Leftrightarrow\left(m+1\right)^2=\left(m-2\right)^2+1\)

\(\Leftrightarrow6m=4\)

\(\Rightarrow m=\dfrac{2}{3}\)

\(d\left(O;d\right)=\dfrac{\left|\left(m-2\right)\cdot0+\left(-1\right)\cdot0+3\right|}{\sqrt{\left(m-2\right)^2+1}}=\dfrac{3}{\sqrt{\left(m-2\right)^2+1}}\)

Để d=1 thì \(\sqrt{\left(m-2\right)^2+1}=3\)

=>(m-2)^2+1=9

=>(m-2)^2=8

=>\(m=\pm2\sqrt{2}+2\)

a: Thay x=2 và y=-1 vào (d), ta được:

2(m-2)+5=-1

=>2(m-2)=-6

=>m-2=-3

=>m=-1

b: (d): y=(m-2)x+5

=>(m-2)x-y-5=0

Khoảng cách từ O đến (d) là:

\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\left(m-2\right)+0\left(-1\right)-5\right|}{\sqrt{\left(m-2\right)^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{\left(m-2\right)^2+1}}\)

Để d(O;(d))=3 thì \(\dfrac{5}{\sqrt{\left(m-2\right)^2+1}}=3\)

=>\(\sqrt{\left(m-2\right)^2+1}=\dfrac{5}{3}\)

=>\(\left(m-2\right)^2+1=\dfrac{25}{9}\)

=>\(\left(m-2\right)^2=\dfrac{16}{9}\)

=>\(\left[{}\begin{matrix}m-2=\dfrac{4}{3}\\m-2=-\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{10}{3}\\m=\dfrac{2}{3}\end{matrix}\right.\)

1: Thay x=1 và y=-1 vào (d), ta được:

\(1\left(m-2\right)+m+1=-1\)

=>2m-1=-1

=>m=0

Khi m=0 thì (d): \(y=\left(0-2\right)x+0+1=-2x+1\)

2: Để (d)//(d') thì \(\left\{{}\begin{matrix}m-2=-3\\m+1< >1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=-1\\m< >0\end{matrix}\right.\)

=>m=-1

3:

(d): y=(m-2)x+m+1

=>(m-2)x-y+m+1=0

Khoảng cách từ O đến (d) là:

\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-2\right)+0\cdot\left(-1\right)+m+1\right|}{\sqrt{\left(m-2\right)^2+\left(-1\right)^2}}=\dfrac{\left|m+1\right|}{\sqrt{\left(m-2\right)^2+1}}\)

Để d(O;(d))=1 thì \(\dfrac{\left|m+1\right|}{\sqrt{\left(m-2\right)^2+1}}=1\)

=>\(\sqrt{\left(m-2\right)^2+1}=\sqrt{\left(m+1\right)^2}\)

=>\(\left(m-2\right)^2+1=\left(m+1\right)^2\)

=>\(m^2-4m+4+1=m^2+2m+1\)

=>-4m+5=2m+1

=>-6m=-4

=>m=2/3(nhận)

\(a,\) Gọi điểm cố định (d) luôn đi qua là \(A\left(x_0;y_0\right)\)

\(\Leftrightarrow y_0=\left(m-2\right)x_0+2\Leftrightarrow mx_0-2x_0+2-y_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\2-2x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow A\left(0;2\right)\)

Vậy \(A\left(0;2\right)\) là điểm cố định mà (d) lun đi qua

\(b,\) PT giao Ox,Oy: \(y=0\Leftrightarrow x=\dfrac{2}{2-m}\Leftrightarrow B\left(\dfrac{2}{2-m};0\right)\Leftrightarrow OB=\dfrac{2}{\left|m-2\right|}\\ x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)

Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=1\)

Áp dụng HTL: \(\dfrac{1}{OH^2}=1=\dfrac{1}{OB^2}+\dfrac{1}{OC^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)

\(\Leftrightarrow m^2-4m+4+1=4\\ \Leftrightarrow m^2-4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{3}\\m=2-\sqrt{3}\end{matrix}\right.\)

\(c,\) Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)

Đặt \(OH^2=t\)

\(\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-4m+5}{4}\Leftrightarrow t=\dfrac{4}{\left(m-2\right)^2+1}\le\dfrac{4}{0+1}=4\\ \Leftrightarrow OH\le2\\ OH_{max}=2\Leftrightarrow m=2\)

(d): \(y=\left(m^2+3\right)x+4\)

=>\(\left(m^2+3\right)x-y+4=0\)

Khoảng cách từ O(0;0) đến (d) là:

\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m^2+3\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m^2+3\right)^2+\left(-1\right)^2}}\)

\(=\dfrac{4}{\sqrt{\left(m^2+3\right)^2+1}}\)

\(m^2+3>=3\forall m\)

=>\(\left(m^2+3\right)^2>=9\forall m\)

=>\(\left(m^2+3\right)^2+1>=10\forall m\)

=>\(\sqrt{\left(m^2+3\right)^2+1}>=\sqrt{10}\forall m\)

=>\(\dfrac{4}{\sqrt{\left(m^2+3\right)^2+1}}< =\dfrac{4}{\sqrt{10}}\forall m\)

=>\(d\left(O;\left(d\right)\right)< =\dfrac{4}{\sqrt{10}}\forall m\)

Vậy: Khoảng cách từ O(0;0) đến (d) lớn nhất bằng \(\dfrac{4}{\sqrt{10}}=\dfrac{4\sqrt{10}}{10}=\dfrac{2\sqrt{10}}{5}\) khi m=0

a: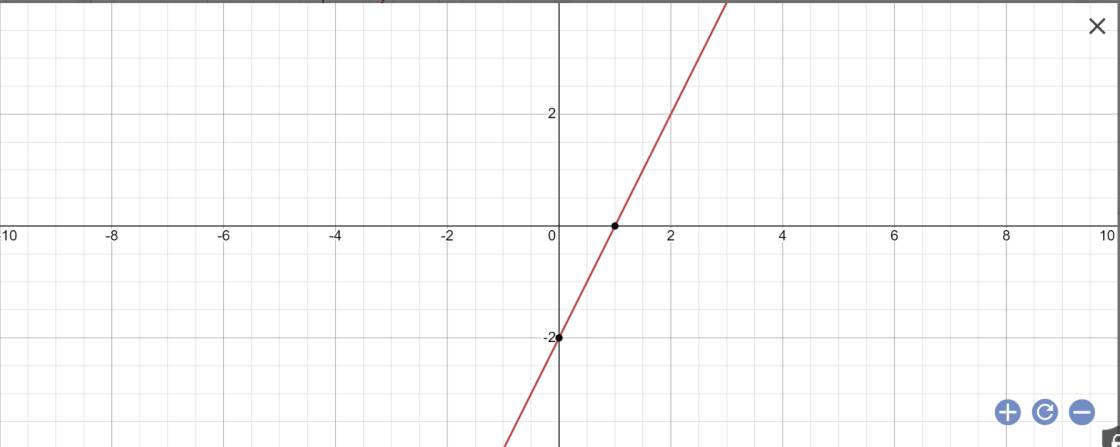 

b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)

=>m+1=2

=>m=1

c:

(d'): y=(m+1)x+6

=>(m+1)x-y+6=0

Khoảng cách từ O đến (d') là:

\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)

\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)

Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)

=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)

=>\(\left(m+1\right)^2+1=2\)

=>\(\left(m+1\right)^2=1\)

=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)