16 x 65 x 82:(43x 25x 16)

Những câu hỏi liên quan
Giải phương trình: \(4x^3-25x^2+43x+x\sqrt{3x-2}=22+\sqrt{3x-2}\).
thực hiện phép tính
a)\(\dfrac{1}{x-5x^2}\)-\(\dfrac{25x-15}{25x^2-1}\)
b)(-\(\dfrac{1}{x^2-4x}+\dfrac{2}{16-x^2}-\dfrac{-1}{4x+16}\))\(\div\dfrac{1}{4x}\)
`a)1/[x-5x^2]-[25x-15]/[25x^2-1]`
`=[-(5x+1)-x(25x-15)]/[x(5x-1)(5x+1)]`
`=[-5x-1-25x^2+15x]/[x(5x-1)(5x+1)]`
`=[-25x^2+10x-1]/[x(5x-1)(5x+1)]`
`=[-(5x-1)^2]/[x(5x-1)(5x+1)]`
`=[1-5x]/[x(5x+1)]`
________________________________________________-
`b)(-1/[x^2-4x]+2/[16-x^2]-[-1]/[4x+16]):1/[4x]`
`=[-4(x+4)-8x+x(x-4)]/[4x(x-4)(x+4)].4x`
`=[-4x-16-8x+x^2-4x]/[(x-4)(x+4)]`
`=[x^2-16x-16]/[x^2-16]`
Đúng 2
Bình luận (0)
16, giải phương trình.
1, \(\frac{x+5}{65}+\frac{x+10}{60}=\frac{x+15}{55}+\frac{x+20}{50}\)
2, \(\frac{x+91}{81}+\frac{x+92}{82}+\frac{x+93}{83}=3\)
3, \(\frac{59-x}{19}+\frac{58-x}{18}=\frac{57-x}{17}+\frac{56-x}{16}\)
4, \(\frac{x}{15}+\frac{x+1}{16}+\frac{x+2}{17}+\frac{x+3}{18}+\frac{x+4}{19}=5\)
(16 x 6+ 16 x3 + 16) – 12 x 65 – 12 x 3 – 2 x12
Giải hộ mình với
Ta có:
\(\left(16\times6+16\times3+16\right)-12\times65-12\times3-2\times12\)
\(=16\times\left(6+3+1\right)-\left(12\times65+12\times3+2\times12\right)\)
\(=16\times10-12\left(65+3+2\right)\)
\(=160-12\times80\)
\(=160-960\)
\(=-800\)
theo mình nhớ thì toán lớp 3 ko có số âm nên bạn coi thử đề có sai ko ???
sai đề không em ơi, kết quả ra số âm, mà số âm ko học ở lớp 3
sai đề vì lớp 3 đâu có hok số âm đâu
Xem thêm câu trả lời
Tìm x:
\(\sqrt{9x-27}+\sqrt{25x-75}=16\)\(16\)
ĐK: \(x\ge5\)
\(3\sqrt{x-3}+5\sqrt{x-5}=1616.\)
Đặt \(\sqrt{x-3}=a,\sqrt{x-5}=b\left(a,b\ge0\right)\)
Ta được hệ pt : \(\hept{\begin{cases}3a+5b=1616\\a^2-b^2=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=\frac{1616-3a}{5}\\a^2-\left(\frac{1616-3a}{5}\right)^2-2=0\left(1\right)\end{cases}}\)
Giải (1)
\(\left(1\right)\Leftrightarrow25a^2-\left(1616-3a\right)^2-50=0\)
Giải cái này là ra nghiệm nhé :))))) SỐ TO NÊN LƯỜI :P
Giải phương trình:
\(4x^2-25x^2+43x+x\sqrt{3x-2}=22+\sqrt{3x-2}\)
Điều kiện: 3x - 2 \(\ge0\) <=> x \(\ge\frac{2}{3}\)
pt <=> \(22x^2-43x^2+43x+x\sqrt{3x-2}-\sqrt{3x-2}-22=0\)
<=> \(\left(22x^2-22\right)+\left(43x-43x^2\right)+\left(x\sqrt{3x-2}-\sqrt{3x-2}\right)=0\)
<=> \(22.\left(x-1\right)\left(x+1\right)+43x\left(1-x\right)+\sqrt{3x-2}.\left(x-1\right)=0\)
<=> \(\left(x-1\right).\left(22x+22-43x+\sqrt{3x-2}\right)=0\)
<=> x-1 = 0 hoặc \(22-21x+\sqrt{3x-2}=0\)
+) x - 1 = 0 => x = 1 (thoả mãn)
+) \(22-21x+\sqrt{3x-2}=0\Leftrightarrow\sqrt{3x-2}=21x-22\) (*)
Điều kiện : 21x - 22 \(\ge\) 0
(*) <=> 3x - 2 = (21x - 22)2 <=> 3x - 2 = 441x2 - 924x + 484 <=> 441x2 - 927x + 486 = 0
Vì 441 - 927 + 486 = 0 => ptrinh có 1 nghiệm x1 = 1 (loại); x2 = \(\frac{486}{441}\) (thoả mãn)
vậy phương trình đã cho có 2 nghiệm là: x = 1; x = \(\frac{486}{441}\)
Đúng 0
Bình luận (0)
Tính hợp lí :
a= 39 x 118 +29 x 82
b = 37 x 39 + 78 x 14 + 13 x 85 + 52 x 55
c= 368 : 16 + 752 : 16 + 480 : 16
d= 5 x 11 x 18 + 9 x 31 x 10 + 4 x 29 x 45
a) \(39\times118+29\times82\)
\(=39\times2\times59+29\times2\times41\)
\(=2\times\left(39\times59+29\times41\right)\)
\(=2\times\left(2301+1189\right)\)
\(=2\times3490\)
\(=6980\)
b) \(37\times39+78\times14-13\times85-52\times55\)
\(=37\times3\times13+6\times13\times14+13\times85-4\times13\times55\)
\(=13\times\left(37\times3+6\times14+85-4\times55\right)\)
\(=13\times\left(111+84+85-220\right)\)
\(=13\times\left(280-220\right)\)
\(=13\times60\)
\(=780\)
c) \(368:16+752:16+480:16\)
\(=\left(368+752+480\right):16\)
\(=\left(1120+480\right):16\)
\(=1600:16\)
\(=100\)
d) \(5\times11\times18+9\times31\times10+4\times29\times45\)
\(=5\times11\times9\times2+9\times31\times10+2\times2\times29\times5\times9\)
\(=10\times9\times11+10\times9\times31+10\times29\times2\times9\)
\(=90\times11+90\times31+90\times29\times2\)
\(=90\times\left(11+31+29\times2\right)\)
\(=90\times\left(42+58\right)\)
\(=90\times100\)
\(=9000\)
Đúng 1
Bình luận (0)
Phương trình
4
3
x
-
2
16
có nghiệm là A.
x
3
4
B.
x
5
C.
x
4
3
D.
x
3
Đọc tiếp
Phương trình 4 3 x - 2 = 16 có nghiệm là
A. x = 3 4
B. x = 5
C. x = 4 3
D. x = 3
x + 59 =82 - 16
x+59=82-16
x+59=66
x =66-59
x =7
tk mk nha!mk tk bn rooig đó
Đúng 0
Bình luận (0)
x + 59 = 82 - 16
x + 59 = 66
x = 66 - 59
x = 7
Đúng 0
Bình luận (0)
x + 59 =82 - 16
x + 59 =66
x = 66 - 59
x = 7
Đúng 0
Bình luận (0)
Xem thêm câu trả lời























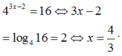 .
.


