x - 3xy - 3y = -4
Tim x, y
Tim (x,y) nguyen biet a) x + y = x : y = xy b) 2x + 3y + 3xy = 7
b) Ta có : 2x + 3y + 3xy = 7
=> 3y(1 + x) + 2x + 2 = 9
=> 3y(1 + x) + 2(x + 1) = 9
=> (x + 1)(3y + 2) = 9
=> x + 1 và 3y + 2 thuộc Ư(9) = {-9;-3;-1;1;3;9}
+) x + 1 = -9 thì 3y + 2 = -1
=> x = -10 ; y = -1
+) x + 1 = -1 thì 3y + 2 = -9
=> x = -2 ; y = \(\frac{-11}{3}\) (loại)
+) x + 1 = -3 thì 3y + 2 = -3
=> x = -4 ; y = \(-\frac{5}{3}\)(loại)
+) x + 1 = 1 thì 3y + 2 = 9
=> x = 0 thì y = \(\frac{7}{3}\)(loại)
+ x + 1 = 9 thì 3y + 2 = 1
=> x = 8 ; y = \(-\frac{1}{3}\)(Loại)
+ x + 1 = 3 thì 3y + 2 = 3
=> x = 2 ; y = \(\frac{1}{3}\)(Loại)
Vậy x = -10 và y = -1
Tim (x,y) nguyen biet
a) x + y = x : y = xy
b) 2x + 3y + 3xy = 7
tim GTNN : A =3xy .(x + 3y ) -2xy.(x+4y)-x2(y-1)+y2(1-x)+100
Q=3xy (x+3y) -2xy (x+4y) -x2 (y-1)+y2(1-x)+36
Tim cap x,y de Q dat gia tri nho nhat tim gia tri nho nhat
\(Q=3xy\left(x+3y\right)-2xy\left(x+4y\right)-x^2\left(y-1\right)+y^2\left(1-x\right)+36\)\(\Leftrightarrow Q=3x^2y+9xy^2-2x^2y-8xy^2-x^2y+x^2+y^2-xy^2+36\)\(\Leftrightarrow Q=\left(3x^2y-2x^2y-x^2y\right)+\left(9xy^2-8xy^2-xy^2\right)+x^2+y^2+36\)\(\Leftrightarrow Q=x^2+y^2+36\ge36\forall x;y\)
Dấu " = " xảy ra
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=0\\y^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Vậy Min Q là : \(36\Leftrightarrow x=y=0\)
1) PTTNT
a) x^2 - 4x^2y + 4xy
b)x^2 + 3x + x - 3y
2) Tim GTLN
-2x^2 + 3x - 5
3) tim x,y thuoc z
3xy + 6x - y = 7
Bài 2:
\(A=-2x^2+3x-5\)
\(=-2\left(x^2+\frac{3x}{2}-\frac{5}{2}\right)\)
\(=-2\left(x^2-\frac{3x}{2}+\frac{9}{16}\right)-\frac{31}{8}\)
\(=-2\left(x-\frac{3}{4}\right)^2-\frac{31}{8}\le-\frac{31}{8}\)
Dấu = khi \(-2\left(x-\frac{3}{4}\right)^2=0\Leftrightarrow x-\frac{3}{4}=0\Leftrightarrow x=\frac{3}{4}\)
Vậy \(Max_A=-\frac{31}{8}\Leftrightarrow x=\frac{3}{4}\)
Bài 1:
a)x2-4x2y+4xy
=x(x-4xy+y)
b)đề sai
Bài 3:
3yx + 6x - y = 7
<=> x(3y+6) - (3y+6) = 27
<=> (3y+6)(x+1) = 27
Ta có bảng sau:
| x+1 | 1 | -1 | 3 | -3 | 9 | -9 | 27 | -27 | |
| 3y+6 | 27 | -27 | 9 | -9 | 3 | -3 | 1 | -1 | |
| x | 0 | -2 | 2 | -4 | 8 | -10 | 26 | -28 | |
| y | 7 | -11 | 1 | -5 | -1 | -3 | \(-\frac{5}{3}\) | \(-\frac{7}{3}\) |
Vậy...
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
A. P m i n = 4 3 + 4 3
B. P m i n = 4 3 - 4 3
C. P m i n = 4 3 - 4 9
D. P m i n = 4 3 + 4 9
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
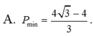
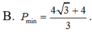
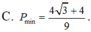
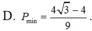
chứng tỏ
a) x2 + 8y2 =( x +2y ) ( x2- 2xy +4y2)
b) (x-y) (x2+xy+y2 ) -3xy (x-y) =( x-y)3
c) (x-3y) (x2 +3xy +9y2 ) - ( 3y +x ) ( 9y2 -3xy + x2) = -54y3
cíu em vớii
\(a,VP=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ =\left(x+2y\right)\left[x^2-x.2y+\left(2y\right)^2\right]\\ =x^3+\left(2y\right)^3=x^3+8y^3=VT\left(đpcm\right)\\ b,VT=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(x-y\right)\\ =x^3-y^3-3xy\left(x-y\right)\\ =x^3-3x^2y+3xy^2-y^3\\ =\left(x-y\right)^3=VP\left(đpcm\right)\)
\(c,VT=\left(x-3y\right)\left(x^2+3xy+9y^2\right)-\left(3y+x\right)\left(9y^2-3xy+x^2\right)\\ =\left(x-3y\right)\left[x^2+x.3y+\left(3y\right)^2\right]-\left(x+3y\right).\left[x^2-x.3y+\left(3y\right)^2\right]\\ =x^3-27y^3-\left(x^3+27y^3\right)\\ =-54y^3=VP\left(đpcm\right)\)
Tìm các số nguyên x,y thoả mãn: 3xy+x-3y\(3xy+x-3y=5\)
\(3xy+x-3y=5\\ \Rightarrow x\left(3y+1\right)-3y-1=5-1\\ \Rightarrow x\left(3y+1\right)-\left(3y-1\right)=4\\ \Rightarrow\left(x-1\right)\left(3y-1\right)=4\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-1,3y-1\in Z\\x-1,3y-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\end{matrix}\right.\)
Ta có bảng:
| x-1 | 1 | 2 | 4 | -1 | -2 | -4 |
| 3y-1 | 4 | 2 | 1 | -4 | -2 | -1 |
| x | 2 | 3 | 5 | 0 | -1 | -3 |
| y | \(\dfrac{5}{3}\left(loại\right)\) | 1 | \(\dfrac{2}{3}\left(loại\right)\) | -1 | \(-\dfrac{1}{3}\left(loại\right)\) | 0 |
Vậy \(\left(x,y\right)\in\left\{\left(3;1\right);\left(0;-1\right);\left(-3;0\right)\right\}\)