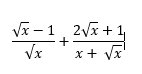 CHứng minh rằng bằng
CHứng minh rằng bằng 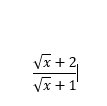

Những câu hỏi liên quan
cho A bằng 2 mũ 1 + 2 mũ 2 +2 mũ 3 + ..... + 2 mũ 120
chứng minh rằng A chia hết cho 7
chứng minh rằng A chia hết cho 31
chứng minh rằng A chia hết cho 217
A = 21 + 22 + 23 + ................ + 2120
Chứng minh chia hết cho 7
A = 21 + 22 + 23 + ................ + 2120
A = (21 + 22 + 23) + (24 + 25 + 26) + ................ + (2118 + 2119 + 2120)
A = 2.(1 + 2 + 4) + 24.(1 + 2 + 4) + ................. + 2118.(1 + 2 + 4)
A = 2.7 + 24 . 7 + ................ + 2118.7
A = 7.(2 + 24 + ........... + 2118)
Chứng minh chia hết cho 31
A = 21 + 22 + 23 + ................ + 2120
A = (21 + 22 + 23 + 24 + 25) + (26 + 27 + 28 + 29 + 210) + ................ + (2116 + 2117 + 2118 + 2119 + 2120)
A = 2.(1 + 2 + 4 + 8 + 16) + 26.(1 + 2 +4 + 8 + 16) + ............. + 2116.(1 + 2 + 4 + 8 + 16)
A = 2.31 + 26.31 + ....... + 2116 . 31
A = 31.(2 + 26 + ........... + 2116)
Đúng 2
Bình luận (0)
A = 21 + 22 + 23 + ................ + 2120
Chứng minh chia hết cho 7
A = 21 + 22 + 23 + ................ + 2120
A = (21 + 22 + 23) + (24 + 25 + 26) + ................ + (2118 + 2119 + 2120)
A = 2.(1 + 2 + 4) + 24.(1 + 2 + 4) + ................. + 2118.(1 + 2 + 4)
A = 2.7 + 24 . 7 + ................ + 2118.7
A = 7.(2 + 24 + ........... + 2118)
Chứng minh chia hết cho 31
A = 21 + 22 + 23 + ................ + 2120
A = (21 + 22 + 23 + 24 + 25) + (26 + 27 + 28 + 29 + 210) + ................ + (2116 + 2117 + 2118 + 2119 + 2120)
A = 2.(1 + 2 + 4 + 8 + 16) + 26.(1 + 2 +4 + 8 + 16) + ............. + 2116.(1 + 2 + 4 + 8 + 16)
A = 2.31 + 26.31 + ....... + 2116 . 31
A = 31.(2 + 26 + ........... + 2116)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
Bài 11. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng AE - AB = AD.AC.
b) Chứng minh rằng ADE = ABC.
c) Chứng minh rằng CH - CE+BH - BD = BC.
d) Giả sử góc A có số do bằng 60°, SABC = 120 cm. Tính SADE.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạngvới ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)
Đúng 0
Bình luận (0)
2/ Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điếm N sao cho AM = AN.
a. Chứng minh rằng Tam giác AMN là tam giác cân.
b. Chứng minh rằng: MN // BC.
c. Chứng minh rằng: tam giác MBC bằng tam giác NCB.
a: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
b: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
c: Xét ΔMBC và ΔNCB có
MB=NC
\(\widehat{MBC}=\widehat{NCB}\)
BC chung
Do đó: ΔMBC=ΔNCB
Đúng 4
Bình luận (3)
b) -Ta có:
\(\widehat{BAC}=180^0-2\widehat{AMN}\) (Tam giác AMN cân tại A).
\(\widehat{BAC}=180^0-2\widehat{ABC}\) (Tam giác ABC cân tại A).
=>\(\widehat{AMN}=\widehat{ABC}\) mà 2 góc này ở vị trí so le trong.
=>MN//BC
Đúng 2
Bình luận (0)
Bài 2:
a) Vì \(AM=AN\) (giả thiết)
\(\Rightarrow\Delta AMN\) cân tại \(A\)
b) Vì \(\Delta AMN\) cân tại \(A\) (chứng minh trên)
\(\Rightarrow\widehat{AMN}=\dfrac{180^o-\widehat{A}}{2}\) (1)
Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
\(\Rightarrow\widehat{ABC}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AMN}=\widehat{ABC}\)
Mà \(2\) góc này ở vị trí đồng vị
\(\Rightarrow MN//BC\)
c) Ta có: \(\left\{{}\begin{matrix}AM+MB=AB\left(M\in AB\right)\\AN+NC=AC\left(N\in AC\right)\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AM=AC\left(cmt\right)\\AB=AC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow MB=NC\)
Xét \(\Delta MBC\) và \(\Delta NCB\) có:
\(MB=NC\left(cmt\right)\)
\(\widehat{MBC}=\widehat{NCB}\) (do \(\Delta ABC\) cân tại \(A\))
\(BC\) là cạnh chung
\(\Rightarrow\Delta MBC=\Delta NCB\left(c.g.c\right)\)
Đúng 2
Bình luận (4)
chứng minh rằng tồn tại vô số các số nguyên tố có dạng 4k+3( chứng minh bằng phản chứng)
Giả sử số các số nguyên tố dạng 4k + 3 là hữu hạn.
Gọi đó là p1, p2, ..., pk.
Xét A = 4*p1*p2*...*pk - 1
A có dạng 4k + 3, vậy theo bổ đề A có ít nhất 1 ước nguyên tố dạng 4k + 3.
Dễ thấy là A không chia hết cho p1, p2, ..., pk, tức không chia hết cho bất cứ số nguyên tố nào có dạng 4k + 3, mâu thuẫn.
Vậy có vô hạn số nguyên tố dạng 4k + 3
**** nhe
Đúng 0
Bình luận (0)
chứng minh bằng phản chứng:
"Cho tam giác ABC có các đường phân giác BE,CF bằng nhau .Chứng minh rằng :tam giác ABC cân tại A"
chứng minh bằng phường pháp phản chứng. chứng minh rằng nếu x^2 =2 thi phường trinh khong có nghiệm trong Q
Chứng minh bằng phản chứng :
Giả sử ngược lại, phương trình \(x^2=2\) có nghiệm \(x\in Q\) , tức là \(x=\frac{p}{q}\) (p,q \(\in Z,q\ne0\)) , \(\frac{p}{q}\) tối giản
Giải \(x^2=2\) được : \(x=\pm\sqrt{2}\)
Do đó: \(\sqrt{2}=\frac{p}{q}\) (Ta chỉ xét trường hợp \(x=\sqrt{2}\) , trường hợp \(x=-\sqrt{2}\) cũng tương tự)
Ta cần chứng minh \(\sqrt{2}\) không là số hữu tỉ.
Ta có : \(\sqrt{2}=\frac{p}{q}\Leftrightarrow p^2=2q^2\left(1\right)\Rightarrow p^2⋮2\Rightarrow p⋮2\) ( vì 2 là số nguyên tố)
Đặt \(p=2k\left(k\in Z\right)\Rightarrow p^2=4k^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow4k^2=2q^2\) nên \(q^2=2k^2\) (3)
Từ (3) lại có \(q^2⋮2\Rightarrow q⋮2\)
p và q cùng chia hết cho 2 nên phân số \(\frac{p}{q}\) không tối giản, trái với giả thiết.
Vậy \(\sqrt{2}\) không là số hữu tỉ, tức là \(x\notin Q\)
Đúng 0
Bình luận (0)
Cho tam giâc ABC có CA bằng CB. Gọi D là trung điểm của AB.
a. Chứng minh rằng: tam giác ADC bằng tam giác BDC
b. Gọi M là trung điểm của CD. Chứng minh rằng: góc CAM bằng góc CBM
c. Trên tia đối của tia DC lấy E sao cho DC bằng DE. Chứng minh rằng: tam giác CDA bằng tam giác EDB
a: Xét ΔCDA và ΔCDB có
CA=CB
DA=DB
CD chung
Do đó: ΔCDA=ΔCDB
b: Xét ΔCAM và ΔCBM có
CA=CB
AM=BM
CM chung
Do đó; ΔCAM=ΔCBM
Suy ra: góc CAM=góc CBM
c: Xét ΔCDA và ΔEDB có
CD=ED
góc CDA=góc EDB
DA=DB
Do đó: ΔCDA=ΔEDB
Đúng 0
Bình luận (0)
chứng minh rằng
Tam giác cân có 2 cạnh bằng nhau 2 góc bằng nhau
B) chứng minh rằng hình vuông có 4 cạnh , có 4 góc , và 4 góc = 90 độ và 4 cạnh = nhau ,
Bạn lên lớp 7,8 đi rồi bạn sẽ học định nghĩa của những hình này !!!
Đúng 0
Bình luận (0)
m chứng minh hộ tao cái định nghĩa với , t éo hiểu tại sao nó như vậy ? hay là mày chỉ biết học vẹt éo C/M dc :)
Đúng 0
Bình luận (0)






















