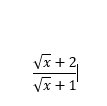\(\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{2\sqrt{x}+1}{x+\sqrt{x}}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ =\dfrac{x+\sqrt{x}-\sqrt{x}-1+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ =\dfrac{x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\left(\text{đ}pcm\right)\)
`(\sqrtx-1)/(\sqrtx)+(2\sqrtx+1)/(x+\sqrtx)`
`=(\sqrtx-1)/(\sqrtx)+(2\sqrtx+1)/(\sqrtx(\sqrtx+1))`
`=((\sqrtx-1)(\sqrtx+1))/(\sqrtx(\sqrtx+1))+(2\sqrtx+1)/(\sqrtx(\sqrtx+1))`
`=(x-1)/(\sqrtx(\sqrtx+1))+(2\sqrtx+1)/(\sqrtx(\sqrtx+1))`
`=(x-1+2\sqrt+1)/(\sqrtx(\sqrtx+1))`
`=(x+2\sqrtx)/(\sqrtx(\sqrtx+1))`
`=(\sqrtx(\sqrtx+2))/(\sqrtx(\sqrtx+1))`
`=(\sqrtx+2)/(\sqrtx+1)` (đpcm)

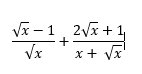 CHứng minh rằng bằng
CHứng minh rằng bằng