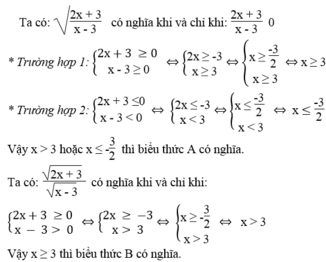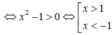tìm x để biểu thức có nghĩa
Đọc tiếp
Những câu hỏi liên quan
Cho các biểu thức:
A
x
+
2
.
x
-
3
B
x
+
2
.
x...
Đọc tiếp
Cho các biểu thức:
A = x + 2 . x - 3 B = x + 2 . x - 3
Tìm x để A có nghĩa. Tìm x để B có nghĩa
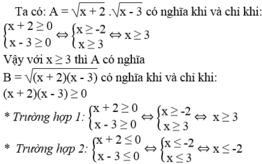
Vậy với x ≥ 3 hoặc x ≤ -2 thì B có nghĩa.
Đúng 0
Bình luận (0)
Cho các biểu thức:
A
2
x
+
3
x
-
3
v
à
B
2...
Đọc tiếp
Cho các biểu thức: A = 2 x + 3 x - 3 v à B = 2 x + 3 x - 3
Tìm x để A có nghĩa. Tìm x để B có nghĩa
cho biểu thức C= x/2x-2 + x^2+1/2-2x^2
a) Tìm x để biểu thức C có nghĩa
b) Rút gọn biểu thức C*c.
c)Tìm giá trị của x để biểu thức có giá trị -0,5
Cho biểu thức M = (x - 3) / (x - 2)
a) Tìm điều kiện để biểu thức M có nghĩa
b) Tìm x để M có giá trị nguyên
a) \(x\ne2\)
b) Ta có : x - 3 chia x - 2 dư -1
Để x - 3 chia hết cho x - 2 thì x - 2 phải là ước của -1
\(\Rightarrow x-2\in\left\{-1;1\right\}\)
\(\Rightarrow x\in\left\{1;3\right\}\)
Đúng 0
Bình luận (0)
tìm x để biểu thức có nghĩa: √[x - 2√(x - 1)]
\(\sqrt{x-2\sqrt{x-1}}\) có nghĩa khi:
\(\left\{{}\begin{matrix}x-1\ge0\\x-2\sqrt{x-1}\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\sqrt{x-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x^2\ge4\left(x-1\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left(x-2\right)^2\ge0\left(LĐ\right)\end{matrix}\right.\)
\(\Rightarrow x\ge1.\)
Đúng 2
Bình luận (2)
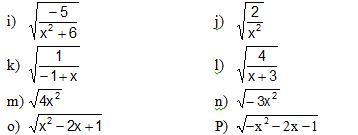Tìm x để biểu thức sau có nghĩa
l, \(x+3>0\Leftrightarrow x>-3\)
m, \(4x^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
n, \(-3x^2\ge0\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
o, \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\Rightarrow\) biểu thức xác định với mọi x.
p, \(-x^2-2x-1=-\left(x+1\right)^2\le0\)
Biểu thức xác định khi \(x+1=0\Leftrightarrow x=-1\)
Đúng 0
Bình luận (0)
i: ĐKXĐ: \(x\in\varnothing\)
j: ĐKXĐ: \(x\ne0\)
k: ĐKXĐ: x>1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x để biểu thức x 2 + x + 1 - 2 3 có nghĩa:
A. ∀ x ∈ R
B. Không tồn tại x
C. ∀ x > 1
D. ∀ x ∈ R\{0}
Biểu thức x 2 + x + 1 - 2 3 có nghĩa khi và chỉ khi: x2 + x + 1 > 0 (luôn đúng với mọi x)
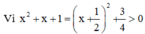
Chọn A
Đúng 0
Bình luận (0)
Tìm x để biểu thức
x
2
+
x
+
1
-
2
3
có nghĩa: A. R B. Không tồn tại x C. x 1 D. x khác 0
Đọc tiếp
Tìm x để biểu thức x 2 + x + 1 - 2 3 có nghĩa:
A. R
B. Không tồn tại x
C. x > 1
D. x khác 0
Chọn A.
Biểu thức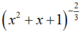 
có nghĩa khi và chỉ khi x2 + x + 1 > 0 ( luôn đúng với mọi x).
Đúng 0
Bình luận (0)
Tìm x để biểu thức
x
2
-
1
1
3
có nghĩa: A.
∀
x
∈
(
-
∞
;
1
]
∪
[
1
;
+
∞
)
B.
∀
x
∈
-
∞...
Đọc tiếp
Tìm x để biểu thức x 2 - 1 1 3 có nghĩa:
A. ∀ x ∈ ( - ∞ ; 1 ] ∪ [ 1 ; + ∞ )
B. ∀ x ∈ - ∞ ; - 1 ∪ 1 ; + ∞
C. ∀ x ∈ - 1 ; 1
D. ∀ x ∈ ℝ \ ± 1
