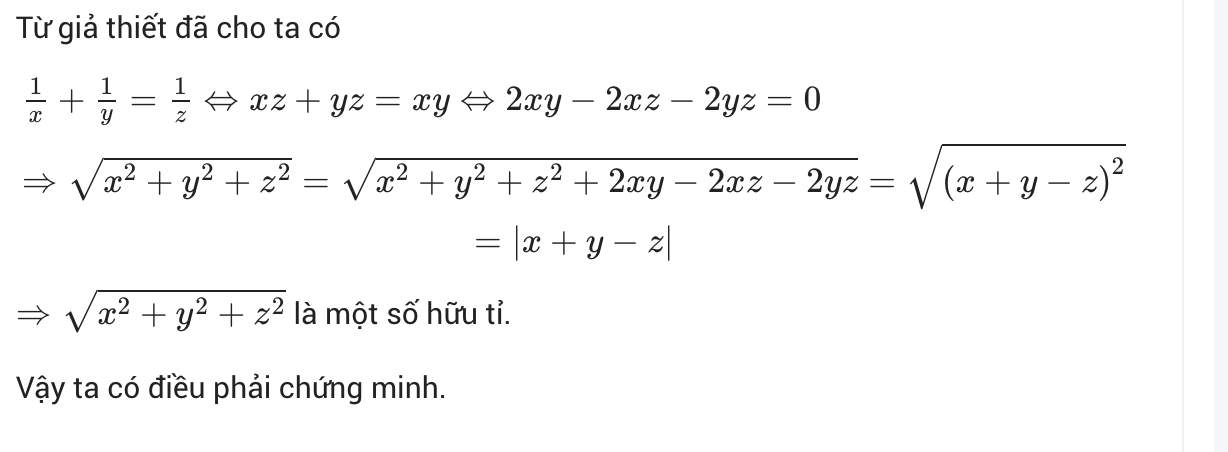Cho x, y là các số hữu tỉ. Chứng minh rằng nếu \(1+\sqrt{x+y+3}=\sqrt{x}+\sqrt{y}\) thì x và y là 2 số chính phương.

Những câu hỏi liên quan
Cho 3 số x,y,\(\sqrt{x}+\sqrt{y}\) là các số hữu tỉ. Chứng minh rằng mỗi số \(\sqrt{x},\sqrt{y}\) đều là số hữu tỉ.
Với x = y \(\ge\)0=> \(\sqrt{x}=\sqrt{y}\) là số hữu tỉ
Với \(x\ne y>0\)
Đặt \(\sqrt{x}+\sqrt{y}=t\) là số hữu tỉ
=> \(\frac{x-y}{\sqrt{x}-\sqrt{y}}=t\Rightarrow\sqrt{x}-\sqrt{y}=\frac{x-y}{t}\) là số hữu tỉ
=> \(\sqrt{x};\sqrt{y}\) là số hữu tỉ
cho 3 số 9x,4y,\(3\sqrt{x}+2\sqrt{y}\) là các số hữu tỉ. Chứng minh rằng \(\sqrt{x},\sqrt{y}\)là các số hữu tỉ.
Ta có \(9x-4y=\left(3\sqrt{x}-2\sqrt{y}\right)\left(3\sqrt{x}+2\sqrt{y}\right)\)là số hữu tỷ
Vì \(\left(3\sqrt{x}-2\sqrt{y}\right)\)(1) là số hữu tỷ nên \(\left(3\sqrt{x}+2\sqrt{y}\right)\)(2) cũng là số hữu tỷ
Lấy (2) - (1) và (2) + (1) ta được
\(\hept{\begin{cases}4\sqrt{y}\\6\sqrt{x}\end{cases}}\)là 2 số hữu tỷ vậy \(\sqrt{x},\sqrt{y}\)là hai số hữu tỷ
Đúng 0
Bình luận (0)
Cho x, y, z là các số hữu tỉ thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{z}\)
Chứng minh rằng \(\sqrt{x^2+y^2+z^2}\) là số hữu tỉ
Các idol dô đây lẹ
Cho x,y là các số hữu tỉ thỏa mãn đẳng thức: \(x^2+y^2+\left(\frac{xy+1}{x+y}\right)^2=2\). Chứng minh rằng \(\sqrt{1+xy}\)là một số hữu tỉ
Đẳng thức đã cho tương đương với
\(x^2+2xy+y^2+\left(\frac{xy+1}{x+y}\right)^2=2+2xy.\)
\(\Leftrightarrow\left(x+y\right)^2+\left(\frac{xy+1}{x+y}\right)^2-2\left(xy+1\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2-2\left(x+y\right).\frac{xy+1}{x+y}+\left(\frac{xy+1}{x+y}\right)^2=0\)
\(\Leftrightarrow\left(x+y-\frac{xy+1}{x+y}\right)^2=0\)
\(\Leftrightarrow x+y-\frac{xy+1}{x+y}=0\)
\(\Leftrightarrow\left(x+y\right)^2=xy+1\)
\(\Leftrightarrow\sqrt{1+xy}=|x+y|\)
Vì x,y là số hữu tỉ nên Vế phải của đẳng thức là số hữu tỉ => Điều phải chứng minh
Chứng minh rằng nếu x,y,z và \(\sqrt{x}+\sqrt{y}+\sqrt{z}\) là các số hữ tỉ thì mỗi số \(\sqrt{x},\sqrt{y},\sqrt{z}\) đều là số hữu tỉ
Cho x;y;\(\sqrt{x}+\sqrt{y}\) là các số hữu tỉ:
Chứng minh rằng: \(\sqrt{x};\sqrt{y}\) hữu tỉ
Lời giải:
Đặt \(\sqrt{x}+\sqrt{y}=a\in\mathbb{Q}\)
\(\Rightarrow \sqrt{x}=a-\sqrt{y}\)
Bình phương 2 vế:
\(x=a^2+y-2a\sqrt{y}\)
\(\Rightarrow 2a\sqrt{y}=a^2+y-x\in\mathbb{Q}\) do \(a,x,y\in\mathbb{Q}\)
Ta thấy \(\left\{\begin{matrix} 2a\sqrt{y}\in\mathbb{Q}\\ 2a\in\mathbb{Q}\end{matrix}\right.\Rightarrow \sqrt{y}\in\mathbb{Q}\)
\(\left\{\begin{matrix} \sqrt{x}+\sqrt{y}\in\mathbb{Q}\\ \sqrt{y}\in\mathbb{Q}\end{matrix}\right.\Rightarrow \sqrt{x}\in\mathbb{Q}\)
Ta có đpcm.
Đúng 0
Bình luận (0)
Cho x, y, z là các số thực dương. Chứng minh rằng:
\(\frac{x}{\sqrt{1+x^2}}+\frac{y}{\sqrt{1+y^2}}+\frac{z}{\sqrt{1+z^2}}\le\frac{3\sqrt{3}}{2}\) nếu x + y + z = xyz
cho x,y,z là 3 số dương và không đồng thời bằng nhau. Chứng minh rằng: Nếu\(\sqrt{x}+\frac{1}{\sqrt{y}}=\sqrt{y}+\frac{1}{\sqrt{z}}=\sqrt{z}+\frac{1}{\sqrt{z}}\) thì xyz=1
Cho \(x;y\) là các số hữu tỉ thoả mãn đẳng thức \(x^2+y^2+\left(\frac{xy+1}{x+y}\right)^2=2\). Chứng minh rằng \(\sqrt{1+xy}\) là một số hữu tỉ.