
giúp em câu b hình với Ạ

Mọi người giúp em câu d hình với ạ. Câu a, b, c em giải được rồi.
Lời giải câu a,b,c của em:
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
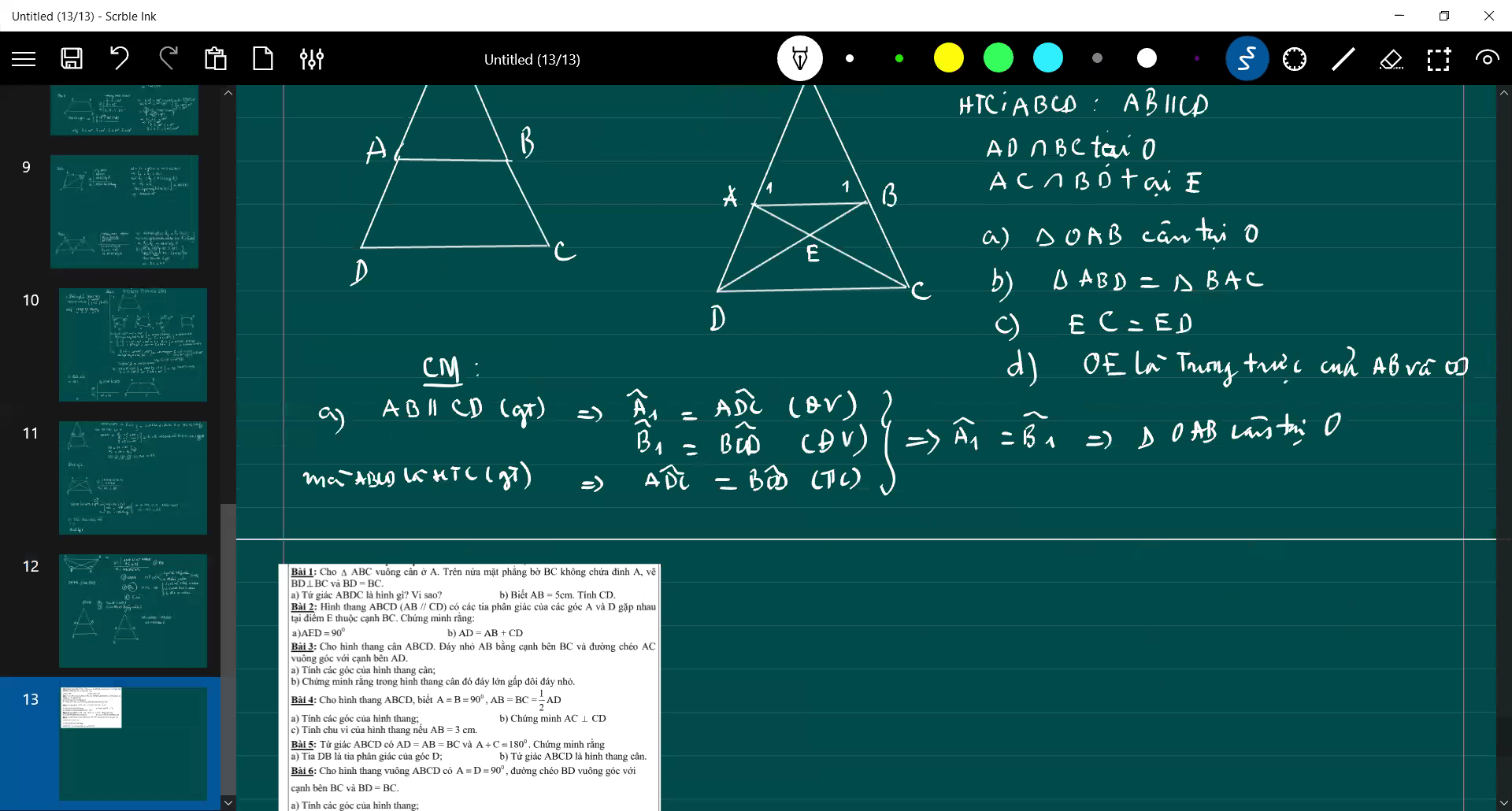
có j thắc mắc thì mn cứ hỏi ạ, em cần trc sáng mai nhé!? ><
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
Ai giúp em bài hàm số với bài hình với ạ nếu rảnh giúp em luôn câu c, bài rút gọn ạ;v

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
Ai giúp em câu hình với (xin luôn ảnh hình với ạ)

ai giúp em câu hình với em cảm ơn ạ ;-;

ai giúp em câu hình với em cảm ơn ạ :((

Ai giúp em câu 1 hình với (xin luôn ảnh hình với ạ)

giúp em câu a hình với ạ
Lời giải:
1)Vì $IB$ là tiếp tuyến của $(O)$ nên $IB\perp OB$
$\Rightarrow \widehat{OBI}=90^0$
$OA=OE=R$ nên tam giác $OAE$ cân tại $O$. Do đó, trung tuyến $OH$ đồng thời là đường cao
$\Rightarrow OH\perp AE$
$\Rightarrow \widehat{OHI}=90^0$
Tứ giác $OBIH$ có tổng 2 góc đối $\widehat{OHI}+\widehat{OBI}=90^0+90^0=180^0$ nên $OBIH$ là tứ giác nội tiếp.
Ta có đpcm.
Giúp em câu 2 bài hình với ạ. Em cảm ơn
a.
Qua S kẻ đường thẳng d song song AB
Do \(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\\S\in\left(SAB\right)\cap\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Gọi E là trung điểm AD, kéo dài AG cắt SD tại F \(\Rightarrow F\) là trung điểm SD (do G là trọng tâm SAD)
AM thuộc AB nên AM cắt SB tại B \(\Rightarrow B'\) trùng B
Trong mp (SCD), qua F kẻ đường thẳng song song CD cắt SC tại C'
\(\Rightarrow C'\) là trung điểm SC (do F là trung điểm SD)
Trong mp (ABCD), kéo dài AB và CE cắt nhau tại H
3 mp (SCE), (ABCD), (AGM) cắt nhau theo 3 giao tuyến phân biệt AB, CE, C'G, mà AB và CE cắt nhau tại H \(\Rightarrow\) 3 đường thẳng đồng quy tại H (theo t/c giao tuyến 3 mp cắt nhau)
Hay C',G,H thẳng hàng
\(AE||CB\) ; \(AE=\dfrac{1}{2}AD=\dfrac{1}{2}CB\Rightarrow\) AE là đường trung bình tam giác HCB
\(\Rightarrow A\) là trung điểm BH và E là trung điểm CH
\(\Rightarrow G\) là trọng tâm tam giác SCH
\(\Rightarrow\dfrac{HG}{HC'}=\dfrac{2}{3}\) (1)
Theo giả thiết \(MB=2MA\Rightarrow AB-MA=2MA\Rightarrow MA=\dfrac{1}{3}AB=\dfrac{1}{3}AH\)
\(\Rightarrow\dfrac{HM}{BH}=\dfrac{AH+AM}{2AH}=\dfrac{AH+\dfrac{1}{3}AH}{2AH}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{HG}{HC'}=\dfrac{HM}{BH}\Rightarrow MG||BC'\)
Hay \(MG||B'C'\) (do B trùng B')