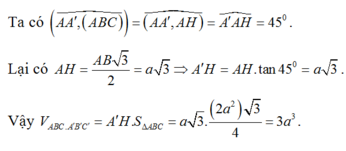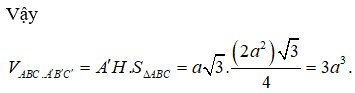Cho lăng trụ ABCA'B'C' có cạnh bên = a, d(C,(C'AB)) = \(\dfrac{a\sqrt{3}}{2}\). Tính ((C'AB)(ABC)

Những câu hỏi liên quan
1. Cho lăng trụ đứng ABC.ABC là tam giác đều cạnh a, số đo của góc giữa 2 mặt phẳng ( CAB ) và ( ABC ) 60. Tính thể tích khối lăng trụ ABC.ABC2. Một người gửi ngân hàng 200 triệu đồng với lãi suất không đổi r 8% / năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu ( gọi là lãi suất kép ). Hỏi sau bao nhiêu năm người đó có ít nhất 500 triệu đồnggiúp mình vs ạ mình cần gấp
Đọc tiếp
1. Cho lăng trụ đứng ABC.A'B'C' là tam giác đều cạnh a, số đo của góc giữa 2 mặt phẳng ( C'AB ) và ( ABC ) = 60. Tính thể tích khối lăng trụ ABC.A'B'C'
2. Một người gửi ngân hàng 200 triệu đồng với lãi suất không đổi r = 8% / năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu ( gọi là lãi suất kép ). Hỏi sau bao nhiêu năm người đó có ít nhất 500 triệu đồng
giúp mình vs ạ mình cần gấp
1.
TRẢ LỜI:chọn C
Gọi M là trung điểm của BC
=> AM ⊥⊥ BC (1)
Ta có {BC ⊥AMBC⊥AA'⇒ BC ⊥ A'M (2)BC ⊥AMBC ⊥AA'⇒ BC ⊥ A'M (2)
Mặt khác (ABC) ∩(A'BC) = BC (3)ABC ∩A'BC = BC (3)
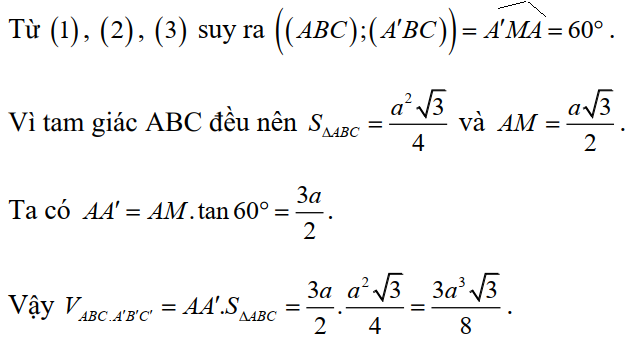
Đúng 0
Bình luận (0)
Cho lăng trụ ABCA'B'C', cạnh đáy bằng, AA' = \(\dfrac{\text{a}\sqrt{\text{2}}}{\text{2}}\)
a, (A'C,(ABC))
b, (A'C,(ABB'A'))
c, (BA'(BCC'B'))
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác vuông cân tại A, mặt bên BCCB là hình vuông cạnh
2
α
. Thể tích của khối lăng trụ ABCABC bằng
Đọc tiếp
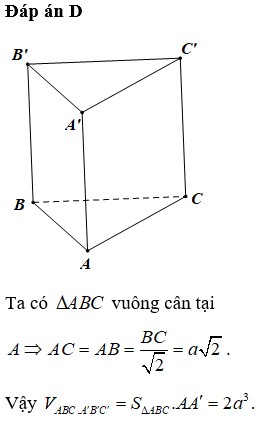
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2 α . Thể tích của khối lăng trụ ABCA'B'C' bằng
![]()
![]()

![]()
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác vuông cân tại A, mặt bên BCCB là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ A.
V
a
3
B.
V
a
3
2
C.
V
2
a
3
3
D.
V
2...
Đọc tiếp
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ
A. V = a 3
B. V = a 3 2
C. V = 2 a 3 3
D. V = 2 a 3
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{ABC}.A'B'C'=AA'.S_{ABC}=2a.\dfrac{a^2\sqrt{3}}{2}=a^3\sqrt{3}\)
Chọn A
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho lăng trụ ABCABC có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A trên (ABC) là trung điểm H của BC, góc giữa AA và (ABC) bằng
45
0
. Tính thể tích V của khối lăng trụ ABCABC.
Đọc tiếp
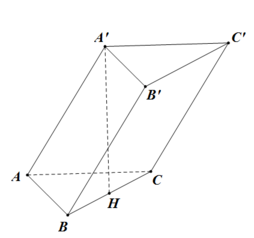
Cho lăng trụ ABCA'B'C' có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A' trên (ABC) là trung điểm H của BC, góc giữa AA' và (ABC) bằng 45 0 . Tính thể tích V của khối lăng trụ ABCA'B'C'.
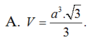
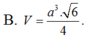
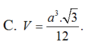
![]()
Cho lăng trụ ABCABC có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A trên (ABC) là trung điểm H của BC, góc giữa AA và (ABC) bằng
45
°
. Tính thể tích V của khối lăng trụ ABCABC A.
V
a
3
3
3
B.
V
a
3
6...
Đọc tiếp
Cho lăng trụ ABCA'B'C' có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A' trên (ABC) là trung điểm H của BC, góc giữa AA' và (ABC) bằng 45 ° . Tính thể tích V của khối lăng trụ ABCA'B'C'
A. V = a 3 3 3
B. V = a 3 6 4
C. V = a 3 3 12
D. V = 3 a 3
cho lăng trụ ABCA'B'C' .Có đáy ABC là tam giác đều cạnh a góc giữa cạnh đáy và mặt bên là 45 độ .Hình chiếu của A lên (A'B'C') là trung điểm của A'B'.Gọi M là trung điểm của B'C' .Tính thể tích lăng trụ và Cos(A'M,AB')
cho hình lăng trụ ABCA'B'C' đáy là tam giác đều cạnh 2a✓2, AA'=a✓3. hình chiếu của A' lên (ABC) trùng với trọng tâm của tam giác ABC. tính thể tích ABCA'B'C'