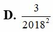Rút gọn biểu thức

Những câu hỏi liên quan
a. Khi rút gọn biểu thức hửu tỉ có tìm điều kiện xác định không ? từ đó hãy rút gọn biểu thức M left(dfrac{1}{1+x}+dfrac{2x}{1-x^{text{2}}}right):left(dfrac{1}{x}-1right)b. Khi rút gọn biểu thức chứa căn có tìm điều kiện không ? từ đó hãy rút gọn biểu thức N dfrac{sqrt{x}+1}{sqrt{text{x}}-2}+dfrac{2sqrt{x}}{sqrt{x}+2}+dfrac{2+5sqrt{x}}{4-x}
Đọc tiếp
a. Khi rút gọn biểu thức hửu tỉ có tìm điều kiện xác định không ? từ đó hãy rút gọn biểu thức M = \(\left(\dfrac{1}{1+x}+\dfrac{2x}{1-x^{\text{2}}}\right):\left(\dfrac{1}{x}-1\right)\)
b. Khi rút gọn biểu thức chứa căn có tìm điều kiện không ? từ đó hãy rút gọn biểu thức N = \(\dfrac{\sqrt{x}+1}{\sqrt{\text{x}}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
Đúng 3
Bình luận (2)
Rút gọn biểu thức rồi tìm giá trị x để biểu thức rút gọn âm:
\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}\)
\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}\)
Để biểu thức trên nhận giá trị âm khi \(\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}< 0\)
\(\Rightarrow x^3-2x^2-4x+8< 0\)do \(\left(x-2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)-2x\left(x+2\right)< 0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)^2< 0\Leftrightarrow x< -2\)
Đúng 1
Bình luận (0)
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
rút gọn biểu thức sau rồi tìm giá trị x dể biểu thức rút gọn duơng
(x^2-4x+4)/(x^3-2x^2-(4x-8))
Rút gọn biểu thức sau, rồi tìm giá trị của x để giá trị của biểu thức rút gọn là 1 số dương:
\(\dfrac{8-2x}{x^2+x-20}\)
\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)
Đúng 0
Bình luận (0)
Cho biểu thức 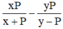 . Thay
. Thay 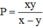 vào biểu thức đã cho rồi rút gọn biểu thức.
vào biểu thức đã cho rồi rút gọn biểu thức.
Thay 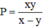 vào biểu thức ta được:
vào biểu thức ta được:
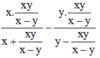
Ta có:
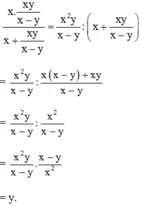
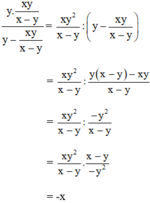
Vậy giá trị biểu thức bằng y – (-x) = x + y.
Đúng 0
Bình luận (0)
Rút gọn biểu thức:
A
a
2
+
2
a
2
a
+
10
+
a
−
5
a
+
50
−
5
a
2...
Đọc tiếp
Rút gọn biểu thức: A = a 2 + 2 a 2 a + 10 + a − 5 a + 50 − 5 a 2 a ( a + 5 ) .
a) Tìm điều kiện xác định của biểu thức A;
b) Rút gọn biểu thức;
c) Tính giá trị của biểu thức tại a = -1
d) Tìm giá trị của a để A = 0.
a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)
Đúng 0
Bình luận (0)
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
a) Thay phân thức
P
uv
u
−
v
vào biểu thức
A
uP
u
+
P
−
vP
v
−
P
rồi rút gọn;b) Thay hai phân thức
P
2
mn...
Đọc tiếp
a) Thay phân thức P = uv u − v vào biểu thức A = uP u + P − vP v − P rồi rút gọn;
b) Thay hai phân thức P = 2 mn m 2 + n 2 và Q = 2 mn m 2 + n 2 vào biểu thức B = P 2 Q 2 P 2 − Q 2 rồi rút gọn;
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
Đúng 0
Bình luận (0)
Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Đọc tiếp
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
![]()
![]()
![]()