A = (2 + √3)/[√(7 - 4√3)] - (2 - √3)/[√(7 + 4√3)]
= (2 + √3)/(2 - √3) - (2 - √3)(2 + √3)
= (2 + √3)² - (2 - √3)²
= 4 + 4√3 + 3 - 4 + 4√3 - 3
= 8√3
A = (2 + √3)/[√(7 - 4√3)] - (2 - √3)/[√(7 + 4√3)]
= (2 + √3)/(2 - √3) - (2 - √3)(2 + √3)
= (2 + √3)² - (2 - √3)²
= 4 + 4√3 + 3 - 4 + 4√3 - 3
= 8√3
Rút gọn biểu thức
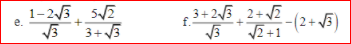
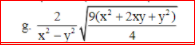
tìm điều kiện và rút gọn biểu thức:
tìm x để biểu thức = 5/3
Rút gọn các biểu thức sau:
A = \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\)
C = \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}\)
E = \(\dfrac{x\sqrt{x}+1}{\sqrt{x}+1}\)
Bài 1 Rút gọn biểu thức:
a) \(\dfrac{\sqrt{3-\sqrt{5}.}\left(3+\sqrt{5}\right)}{\sqrt{10}+\sqrt{2}}\)
b) \(\dfrac{4}{\sqrt{3}+1}+\dfrac{1}{\sqrt{3}-1}+\dfrac{6}{\sqrt{3}-3}\)
Rút gọn các biểu thức :
a) \(\sqrt{\left(4-\sqrt{15}\right)^2}+\sqrt{15}\)
b) \(\sqrt{7+4\sqrt{3}}-\sqrt{7-4\sqrt{3}}\)
c)\(\sqrt{29+12\sqrt{5}}-\sqrt{29-12\sqrt{5}}\)
Rút gọn biểu thức
\(a.\dfrac{\sqrt{5}-2\sqrt{3}}{\sqrt{5}+\sqrt{3}}-\dfrac{2\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}\)
\(b.x\sqrt{2x+2}+\left(x+1\right)\sqrt{\dfrac{2}{x+1}}-4\sqrt{\dfrac{x+1}{2}}\)
Trục căn thức ở mẫu và rút gọn:
\(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
Rút gọn các biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa):
a. \(\sqrt{18\left(\sqrt{2}-\sqrt{3}\right)^2};\)
b. \(ab\sqrt{1+\dfrac{1}{a^2b^2}};\)
c. \(\sqrt{\dfrac{a}{b^3}+\dfrac{a}{b^4}};\)
d. \(\dfrac{a+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\)
Rút gọn các biểu thức sau (giả thiết các biểu thức chữ đều có nghĩa)
\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\) \(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\) \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}\) \(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}\) \(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}\)