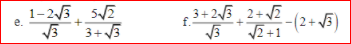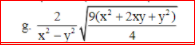\(\left(\dfrac{1}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1-\sqrt{x}}{x+4\sqrt[]{x}+4}\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt[]{x}+2\right)^2}{1-\sqrt{x}}=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
Biểu thức \(=\dfrac{5}{3}\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}}=\dfrac{5}{3}\)
\(\Leftrightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow2\sqrt{x}=6\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)