tìm min hoặc max của x3 + y3 sao cho x + y =1

Những câu hỏi liên quan
1,Cho x,y>0 và xy=2018. Tìm Pmin= 2/x + 1009/y - 2018/(2018x+4y)
2,Cho x,y>0 và x+y=1. Tìm Min B=1/x3+y3 +1/xy
3,Nếu x,y thuộc N* và 2x+3y=53. Tìm max của căn(xy+4)
4,Tìm min P=x^2 +xy +y^2 -3x -3y +2019
5,Cho 0<x<2. Tìm min A= 9x/2-x +2/x
6,Tìm min D= x/y+z + y+z/x + y/x+z + z+x/y + z/x+y + x+y/z
Làm ơn giải giùm mình với, ngay mai kiểm tra rồi.
Cảm ơn nhiều :)))))
Tìm GTLN (max), GTNN (min) của
y
x
3
-
3
x
-
1
khi x
∈
0
;
2
Đọc tiếp
Tìm GTLN (max), GTNN (min) của y = x 3 - 3 x - 1 khi x ∈ 0 ; 2
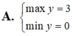
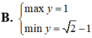
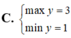
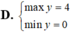
cho số thực x;y thỏa mãn x2+y2=1
tìm min, max của: P=2x+y3
Do \(x^2+y^2=1\Rightarrow-1\le x;y\le1\Rightarrow\left\{{}\begin{matrix}y+1\ge0\\1-y\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y^2\left(y+1\right)\ge0\\y^2\left(1-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y^3\ge-y^2\\y^3\le y^2\end{matrix}\right.\)
Với mọi số thực x ta có:
\(\left\{{}\begin{matrix}\left(x+1\right)^2\ge0\\\left(x-1\right)^2\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x\ge-x^2-1\\2x\le x^2+1\end{matrix}\right.\)
Do đó: \(\left\{{}\begin{matrix}P=2x+y^3\ge-x^2-1-y^2=-2\\P=2x+y^3\le x^2+1+y^2=2\end{matrix}\right.\)
\(P_{min}=-2\) khi \(\left(x;y\right)=\left(-1;0\right)\)
\(P_{max}=2\) khi \(\left(x;y\right)=\left(1;0\right)\)
Đúng 0
Bình luận (0)
tim min của P biết x3+y3-(x2+y2)/(x-1)(y-1) vói x, y là các số thực lớn hơn 1
Đề là: \(P=x^3+y^3-\dfrac{x^2+y^2}{\left(x-1\right)\left(y-1\right)}\)
Hay \(P=\dfrac{x^3+y^3-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}\)
Cái nào em nhỉ?
Đúng 0
Bình luận (1)
\(P=\dfrac{x^3+y^3-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}=\dfrac{x^3-x^2+y^3-y^2}{\left(x-1\right)\left(y-1\right)}=\dfrac{x^2\left(x-1\right)+y^2\left(y-1\right)}{\left(x-1\right)\left(y-1\right)}\)
\(P=\dfrac{x^2}{y-1}+\dfrac{y^2}{x-1}\)
Ta có:
\(\dfrac{x^2}{y-1}+4\left(y-1\right)\ge2\sqrt{\dfrac{4x^2\left(y-1\right)}{y-1}}=4x\)
Tương tự: \(\dfrac{y^2}{x-1}+4\left(x-1\right)\ge4y\)
Cộng vế:
\(P+4\left(x+y\right)-8\ge4\left(x+y\right)\)
\(\Rightarrow P\ge8\)
\(P_{min}=8\) khi \(x=y=2\)
Đúng 1
Bình luận (0)
Tìm GTLN (max), GTNN (min) của hàm số
y
x
3
-
2
x
2
-
4
x
+
8
khi
x
∈
-
1
;
1
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x 3 - 2 x 2 - 4 x + 8 khi x ∈ - 1 ; 1
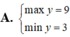
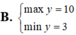
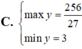
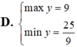
Cho p là số nguyên tố và x, y nguyên dương sao cho x3 + y3 - 3xy = p - 1.
Tìm GTLN của p
Không hiểu sao cái dòng đó lại nhảy như thế. Mình đánh lại.
Giả thiết tương đương với:
\((x+y+1)(x^2+y^2+1-xy-x-y)=p\).
Do x + y + 1 > 1 và p là số nguyên tố nên x + y + 1 = p và \(x^2+y^2+1-x-y-xy=1\Leftrightarrow\left(x+y\right)^2-\left(x+y\right)=3xy\le\dfrac{3}{4}\left(x+y\right)^2\Rightarrow x+y\le4\Rightarrow p\le5\).
Ta thấy 5 là số nguyên tố. Đẳng thức xảy ra khi x = y = 2.
Vậy max p = 5 khi x = y = 2.
Đúng 1
Bình luận (0)
tìm x,y thuộc N* sao cho x3+y3+4(x2+y2)+4(x+y)=16xy
Cho x-y=1. Tìm GTNN của P=x3-y3-x.y
\(x-y=1\Leftrightarrow x=1+y\\ P=\left(x-y\right)\left(x^2+xy+y^2\right)-xy\\ P=x^2+xy+y^2-xy\\ P=x^2+y^2=y^2+2y+1+y^2\\ P=2\left(y^2+y+\dfrac{1}{4}\right)+\dfrac{1}{2}=2\left(y+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)
Dấu \("="\Leftrightarrow y=-\dfrac{1}{2}\Leftrightarrow x=1-\dfrac{1}{2}=\dfrac{1}{2}\)
Đúng 4
Bình luận (0)
x3 - y3 - xy
= (x - y)(x2 + xy + y2) - xy
Thay x - y = 1 vào, ta đc:
= x2 + xy + y2 - xy
= x2 + y2
Ta có: x2 + y2 có giá trị nhỏ nhất khi \(\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 4:
a) Cho x+y=1.Tính x3+y3+3xy
b) Cho x-y=1.Tính x3-y3-3xy
c) Cho x+y=1.Tính x3+y3+3xy(x2+y2)+6x2y2(x+y)
giúp mình với ,gấpppppppppppp
\(a,x+y=1\Leftrightarrow\left(x+y\right)^3=1\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=1\\ \Leftrightarrow x^3+y^3+3xy\cdot1=1\Leftrightarrow x^3+y^3+3xy=1\)
\(b,x^3-y^3-3xy\\ =x^3-3x^2y+3xy^2-y^3-3xy+3x^2y-3xy^2\\ =\left(x-y\right)^3-3xy\left(x-y-1\right)\\ =1^3-3xy\left(1-1\right)=1-0=1\)
\(c,x^3+y^3+3xy\left(x^2+y^2\right)+6x^2y^2\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left[\left(x+y\right)^2-2xy\right]+6x^2y^2\\ =x^2-xy+y^2+3xy-6x^2y^2+6x^2y^2\\ =x^2+2xy+y^2=\left(x+y\right)^2=1\)
Đúng 5
Bình luận (0)


















