Nếu cho AH=3cm,BH=6cm thì BD dài mấy cm

Những câu hỏi liên quan
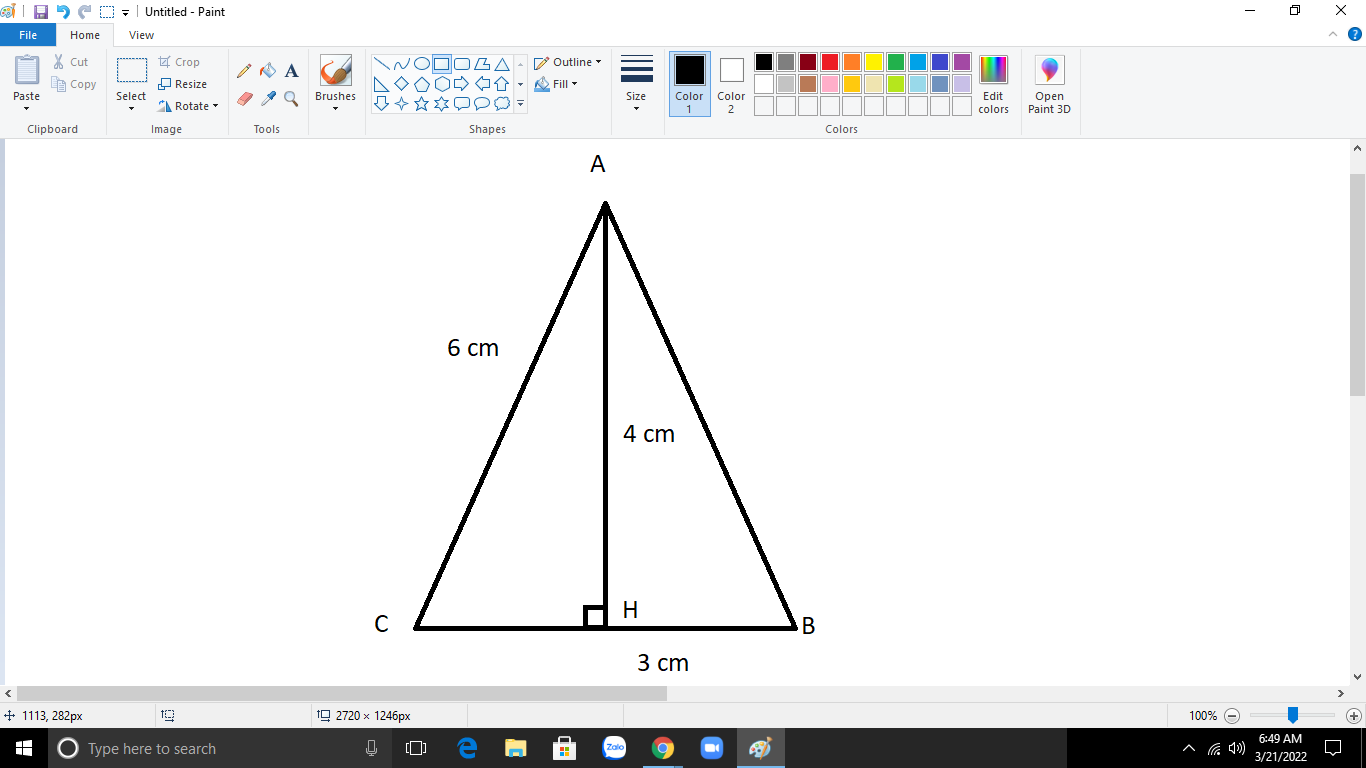
Cho tam giác nhọn ABC kẻ AH vuông góc với BC Biết AH = 4cm BH= 3cm AC=6cm Tính độ dài AB và HC
\(\text{Xét }\Delta AHB\text{ vuông tại H có:}\)
\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)
\(\Rightarrow AB^2=4^2+3^2=16+9=25\left(cm\right)\)
\(\Rightarrow AB=\sqrt{25\left(cm\right)}=5\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow HC^2=6^2-4^2=36-16=20\left(cm\right)\)
\(\Rightarrow HC=\sqrt{20}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho Tam giác ABC vuông tại A cái đường cao AH
a) Biết AB=6cm, BC=10cm.Hãy tính độ dài các đoạn BH,CH ,AH,AC b)Biết AB = căn 3cm,AC =1cm. Hãy tính độ dài các đoạn BC, AH, BH, CH
c) Biết BH=16a, CH=9a (a>0). Hãy tính độ dài các đoạn AH, BC, AB, AC
d) Biết AB=15a, AC= 20a (a>0). Hãy tính độ dài đoạn thẳng AH
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6$ (cm)
$CH=BC-BH=10-3,6=6,4$ (cm)
Tiếp tục áp dụng HTL:
$AH^2=BH.CH=3,6.6,4$
$\Rightarrow AH=4,8$ (cm)
$AC^2=CH.BC=6,4.10=64$
$\Rightarrow AC=8$ (cm)
Đúng 0
Bình luận (0)
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+1^2}=2$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{\sqrt{3}.1}{2}=\frac{\sqrt{3}}{2}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4}}=\frac{3}{2}$ (cm)
$CH=BC-BH=2-\frac{3}{2}=\frac{1}{2}$ (cm)
Đúng 0
Bình luận (0)
3.
$BC=BH+CH=16a+9a=25a$
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH=16a.9a=(12a)^2$
$\Rightarrow AH=12a$ (do $a>0$)
$AB=\sqrt{BH^2+AH^2}=\sqrt{(16a)^2+(12a)^2}=20a$
$AC=\sqrt{CH^2+AH^2}=\sqrt{(9a)^2+(12a)^2}=15a$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AH = 6cm, BH=4,5cm. Tính AB,AC,BC,HC. b) Biết AB = 6cm, BH=3cm. Tính AH,AC,CH
cho tam giác ABC vuông tại A, đường cao AH
a, biết AH = 6cm, BH = 4,5cm. Tính AB, AC, BC, HC
b, biết AB = 6cm, BH = 3cm. Tính AH, AC, CH
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CH=\dfrac{AH^2}{BH}=\dfrac{36}{4,5}=8\left(cm\right)\\AB=\sqrt{4,5\left(4,5+8\right)}=\sqrt{4,5\cdot12,5}=7,5\left(cm\right)\\AC=\sqrt{8\cdot12,5}=10\left(cm\right)\end{matrix}\right.\)
và \(BC=12,5\left(cm\right)\)
\(b,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=CH\cdot BH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=\dfrac{36}{3}=12\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{BC^2-AB^2}{12}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2}\left(cm\right)\\AH=3\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho Tam Giác ABC Vuông tại A;Đ / cao AH ; A, Biết AH=6cm , BH=4.5cm . tính AB,AC,BC,HC ; b, Biết AB=6cm , BH=3cm Tính AH,AC,CH
a) ÁP dụng Pytago ta có: AH2 + HB2 = AB2
=> AB2 = 62 + 4,52 =56,25
=> AB = 7,5
Áp dụng hệ thức lượng ta có: AB2 = BH.BC
=> \(BC=\frac{AB^2}{BH}=12,5\)
=> \(HC=BC-BH=12,5-4,5=8\)
Áp dụng hệ thức lượng ta có:
\(AC^2=HC.BC\)
=> \(AC=\sqrt{HC.BC}=10\)
Đúng 0
Bình luận (0)
b) Áp dụng Pytago ta có: AB2 = BH2 + AH2
=> AH2 = AB2 - BH2 = 27
=> \(AH=3\sqrt{3}\)
Áp dụng hệ thức lượng ta có:
\(AH^2=BH.HC\)
=> \(HC=\frac{AB^2}{BH}=12\)
=> BC = HC + BH = 15
Áp dụng hệ thức lượng ta có:
AC2 = HC.BC
=> \(AC=\sqrt{HC.BC}=6\sqrt{5}\)
Đúng 0
Bình luận (0)
a) Tam giác ABH vuông tại H, áp dụng định lý PyTago
Ta có: \(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4,5^2}=7,5\) (Cm)
Tam giác ABC vuông tại A, áp dụng hệ thức: \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{6^2}-\frac{1}{7,5^2}=\frac{1}{100}\)
\(\Rightarrow AC^2=100\Rightarrow AC=10\) (Cm)
Tam giác ABC vuông tại A, áp dụng định lý Pytago, ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{7,5^2+10^2}=12,5\) (Cm)
\(HC=BC-BH=12,5-4,5=8\) (Cm)
b) Tam giác ABH vuông tại H, áp dụng định lý Pytago, ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{6^2-3^2}=3\sqrt{3}\) (Cm)
Tam giác ABC vuông tại A, áp dụng hệ thức ta được:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{\left(3\sqrt{3}\right)^2}-\frac{1}{6^2}=\frac{1}{108}\)
\(\Rightarrow AC=\sqrt{108}=6\sqrt{3}\) (Cm)
Tam giác ACH vuông tại H, áp dụng định lý Pytago ta có:
\(CH=\sqrt{AC^2-AH^2}=\sqrt{\left(6\sqrt{3}\right)^2-\left(3\sqrt{3}\right)^2}=9\) (Cm)
Đúng 0
Bình luận (0)
1, Tam giác ABC vuông tại A, kẻ đường cao AH
a.Tính AB, AC,BC, HC nếu AH= 6cm, BH= 4,5cm
b.Biết AB= 6cm, HB- 3cm. Tính AH, AC,CH
5, Cho tam giác ABC vuông tại A có AB=21cm, góc C= 40 độ
a.Tính AC
b,Tính BC
Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tg ABC cân tại A có AB=5cm, BC=6cm. Từ A kẻ đường vuông góc đến AH đến BC.
a/CM: BH=HC.
b/Tính độ dài đoạn AH.
c/Gọi G là trọng tâm tg ABC. Trên tia AG lấy điểm D sao cho AG=GD. CG cắt AB tại F. CM: BD=2/3CF và BD>BF.
d/CM: DB+DG>AB.
cho tam giác ABC vuông A, AB=6cm, AC =8cm dướng cao AH đường phân giác BD
AD=3cm, DC=5cm
1, Gọi I là giao điểm của AH và BD CM AB. BI= BD.HB
2, Cm tam giac AID cân
1: Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔABD\(\sim\)ΔHBI
Suy ra: AB/HB=BD/BI
hay \(AB\cdot BI=BD\cdot BH\)
Đúng 0
Bình luận (0)
Cho △ABC vuông tại A, đường cao AH, biết AB= 6cm, BH = 3cm. Tính AH, AC, CH
Xét tam giác ABH vuông tại H, ta có:
AH2 + BH2 = AB2
=> AH2 = 62 - 32
=> AH = \(3\sqrt{3}\) (cm)
Có \(\widehat{BAH}=\widehat{BCA}\) (cùng phụ \(\widehat{HAC}\))
Xét \(\Delta CAH\) và \(\Delta ABH\) có:
+ \(\widehat{BCA}=\widehat{BAH}\)
+ \(\widehat{AHC}=\widehat{BAC}\left(=90^o\right)\)
=> \(\Delta CAH\) \(\sim\) \(\Delta ABH\) (g-g)
=> \(\dfrac{AC}{AH}=\dfrac{AB}{BH}\) => AC = \(6\sqrt{3}\) (cm)
Xét tam giác ABC vuông tại A có AH là đường cao
=> AB2 = BH.BC
=> 62 = 3.BC
=> BC = 12 (cm)
=> CH = 9 (cm)
Đúng 4
Bình luận (1)






















