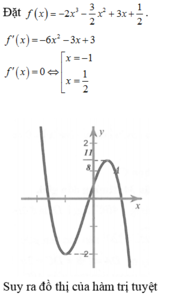
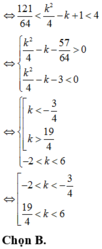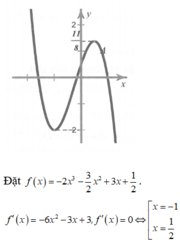tìm k để phương trình x4-2kx2+k2-3=0 có đúng 3 nghiệm phân biệt

Những câu hỏi liên quan
Tìm m để phương trình
x
4
-
2
x
2
+
3
–
m
2
+
2
m
0
có đúng ba nghiệm phân biệt A. m -1 B. m 3 C. -1 m 3 D. Cả A và B
Đọc tiếp
Tìm m để phương trình x 4 - 2 x 2 + 3 – m 2 + 2 m = 0 có đúng ba nghiệm phân biệt
A. m = -1
B. m = 3
C. -1 < m < 3
D. Cả A và B
Chọn D
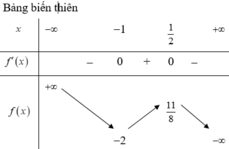
Xét hàm số y = x 4 - 2 x 2 + 3 ( C )
Đồ thị có dạng như hình (1)
x 4 - 2 x 2 + 3 - m 2 + 2 m = 0 có đúng ba nghiệm phân biệt <=> Đường thẳng y = m 2 + 2 m cắt đồ thị C tại ba điểm phân biệt
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực k để phương trình
-
2
x
3
-
3
2
x
2
+
3
x
+
1
2
k
2...
Đọc tiếp
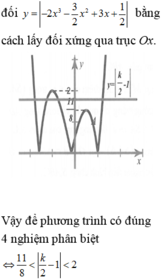
Tìm tất cả các giá trị thực k để phương trình - 2 x 3 - 3 2 x 2 + 3 x + 1 2 = k 2 - 1 có đúng 4 nghiệm phân biệt.
![]()
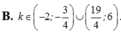
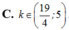
![]()
Tìm tất cả các giá trị thực k để phương trình
-
2
x
3
-
3
2
x
2
+
3
x
+
1
2
k
2...
Đọc tiếp
Tìm tất cả các giá trị thực k để phương trình - 2 x 3 - 3 2 x 2 + 3 x + 1 2 = k 2 - 1 có đúng 4 nghiệm phân biệt
A. k ∈ ∅ .
B. k ∈ - 2 ; - 3 4 ∪ 19 4 ; 6
C. k ∈ 19 5 ; 5
D. k ∈ - 2 ; 1 ∪ 1 ; 19 4
Có bao nhiêu giá trị nguyên của a để phương trình: x 4 + 2 x 2 + a = 0 1 có đúng 3 nghiệm phân biệt
A. 0
B. 1
C. 2
D. 3
Đặt t = x 2 ≥ 0
Phương trình (1) thành t 2 + 2 t + a = 0 1
Phương trình (1) có đúng 3 nghiệm phân biệt
=> phương trình (2) có một nghiệm bằng 0 và nghiệm còn lại dương.
(2) có nghiệm t = 0 ⇔ 0 2 + 2 . 0 + a = 0 ⇔ a = 0
Khi đó phương trình trở thành t 2 + 2 t = 0 ⇔ t = 0 t = − 2 < 0 nên không thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nào của a thỏa mãn bài toán.
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 3 nghiệm phân biệt

Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
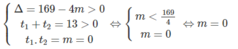
Đúng 0
Bình luận (0)
Tìm m để các phương trình (m+3)x4-(2m-1)x2-3 =0 có:
1/ Một nghiệm
2/ Hai nghiệm phân biệt
3/ Bốn nghiệm phân biệt
Lời giải:
Nếu $m=-3$ thì PT trở thành: $7x^2-3=0$ có nghiệm $x=\pm \sqrt{\frac{3}{7}}$
-------------------------------------------------------------
Nếu $m\neq -3$Đặt $x^2=t$ thì pt trở thành:
$(m+3)t^2-(2m-1)t-3=0(*)$
1. Để pt ban đầu có 1 nghiệm thì PT $(*)$ có nghiệm $t=0$ và nếu có nghiệm còn lại thì nghiệm đó âm.
Để PT $(*)$ có nghiệm $t=0$ thì: $(m+3).0-(2m-1).0-3=0\Leftrightarrow -3=0$ (vô lý)
Do đó không tồn tại $m$ để pt có 1 nghiệm.
2. Để pt ban đầu có 2 nghiệm phân biệt thì PT $(*)$ có 1 nghiệm dương kép hoặc có 1 nghiệm dương và 1 nghiệm âm.
PT có 1 nghiệm dương, 1 nghiệm âm khi \(\left\{\begin{matrix} \Delta (*)=(2m-1)^2+12(m+3)> 0\\ P=\frac{-3}{m+3}<0\end{matrix}\right.\)
\(\Leftrightarrow m>-3\)
PT có nghiệm kép dương $\Leftrightarrow \Delta (*)=(2m-1)^2+12(m+3)=0\Leftrightarrow 4m^2+8m+37=0$ (vô lý)
Vậy $m>-3$
3.
PT ban đầu có 4 nghiệm phân biệt khi PT $(*)$ có 2 nghiệm dương phân biệt
Điều này xảy ra khi \(\left\{\begin{matrix} \Delta (*)=(2m-1)^2+12(m+3)>0\\ S=\frac{2m-1}{m+3}>0\\ P=\frac{-3}{m+3}>0\end{matrix}\right.\Leftrightarrow m< -3\)
Đúng 4
Bình luận (1)
Tìm k để phương trình : x2 – (2k +1)x+ k2 + 4 0 có hai nghiệm phân biệt x1 và x2 thỏa hệ thức: x1^2+ x2^2 63
Đọc tiếp
Tìm k để phương trình : x2 – (2k +1)x+ k2 + 4 = 0 có hai nghiệm phân biệt x1 và x2 thỏa hệ thức: x1^2+ x2^2 = 63
\(\text{Δ}=\left(2k+1\right)^2-4\left(k^2+4\right)\)
\(=4k^2+4k+1-4k^2-16=4k-15\)
Để phương trình có hai nghiệm phân biệt thì 4k-15>0
=>k>15/4
\(x_1^2+x_2^2=63\)
=>(x1+x2)^2-2x1x2=63
=>(2k+1)^2-2(k^2+4)=63
=>4k^2+4k+1-2k^2-8=63
=>2k^2+4k-7-63=0
=>2k^2+4k-70=0
=>k^2+2k-35=0
=>(k+7)(k-5)=0
=>k=-7(loại) hoặc k=5(nhận)
Đúng 0
Bình luận (0)
Tìm tất cả giá trị của m để phương trình
x
4
-
2
(
m
+
1
)
x
2
+
m
2
-
3
0
có 4 nghiệm thực phân biệt?
A
.
(
3
;
+
∞
)
B
.
[
3...
Đọc tiếp
Tìm tất cả giá trị của m để phương trình x 4 - 2 ( m + 1 ) x 2 + m 2 - 3 = 0 có 4 nghiệm thực phân biệt?
A . ( 3 ; + ∞ )
B . [ 3 ; + ∞ )
C . ( 1 ; 6 )
D . [ 1 ; 6 )
Bài 2. Tìm m để phương trình sau có: x4 +2(m – 2)x2 + m2 – 5m + 5 = 0
a) có 4 nghiệm phân biệt b) có 3 nghiệm phận biệt c)có hai nghiệm phân biệt
d) có một nghiệm
e) vô nghiệm