
Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
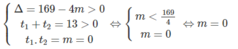

Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
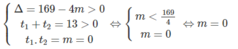
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 4 nghiệm phân biệt
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 2 nghiệm phân biệt
Bài 4:Cho phương trình ẩn x: x2 - (m + 3)x + m = 0
a) Chứng minh rằng với mọi giá trị của m phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình có 2 nghiệm Phân biệt x1, x2 thỏa mãn hệ thức:
x12 + x22 = 6
Cho phương trình bặc hai : (m + 2)x\(^2\)-2(m+1)x+m-4=0. Tìm các giá trị của m để phương trình :
a) có hai nghiệm dương phân biệt ;
b)Có hai nghiệm x\(_1\),x\(_2\) thỏa mãn : 3(x\(_1\)+x\(_2\)) =5x\(_1\).x\(_2\)
Cho phương trình ( m + 1 ) x 2 – 2 ( m + 1 ) x + 1 = 0 . Tìm các giá trị của m để phương trình có hai nghiệm phân biệt
A. m > 0
B. m < −1
C. −1 < m < 0
D. Cả A và B đúng
cho phương trình : x2 + 2(m-1)x - m + 1 = 0
a) tìm các giá trị của m để phương trình có một nghiệm < 1 và 1 nghiệm > 1
b) tìm các giá trị của m để phương trình có hai nghiệm phân biệt < 2
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
Cho phương trình: x2 –(m+1)x+2m-3 =0 (1)
+ Chứng minh rằng phương trình trên luôn có 2 nghiệm phân biệt với mọi giá trị của m.
+ Tìm giá trị của m để phương trình (1) có nghiệm bằng 3.
Cho phương trình : x2 – (m + 1)x + 2m - 3 = 0
a) + Chứng minh rằng phương trình trên luôn có 2 nghiệm phân biệt với mọi giá trị của m.
+ Tìm giá trị của m để phương trình (1) có nghiệm bằng 3.