Câu 1:

Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt

Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))

Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)

Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)

\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)

Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)

Bài 2:

Bạn tham khảo ở đây:

Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến

Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)

 \(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)

Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)

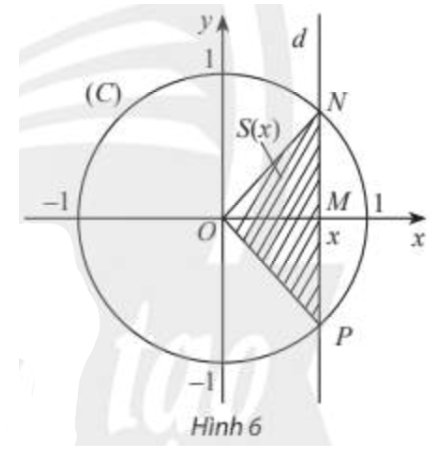
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y =  \pm \sqrt {1 - {x^2}} \).

Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).

Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).

\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).

b) Xét hàm số  \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).

ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow  - 1 \le x \le 1\)

Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).

Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).

Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) =  - 0.\sqrt {1 - {0^2}}  = 0\)

Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)

Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).

c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}}  = 0\)

\(\mathop {\lim }\limits_{x \to  - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to  - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) =  - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}}  = 0\)

a, (d) cắt trục hoành tại A(x_A;0) và trục tung B(0;x_B)

Vì A thuộc (d) nên \(0=-2x_A+4\Leftrightarrow x_A=2 \Rightarrow A(2;0)\)

Vì B thuộc (d) nên \(y_B=-2.0+4=4\Rightarrow B(0;4)\)

Vậy A(2;0) và B(0;4) là hai điểm cần tìm.

b, Gọi C(x_c;y_c) là điểm có hoành độ bằng tung độ

⇒ x_c = y_c = a. Vì C thuộc (d) nên \(a=-2a+4\Leftrightarrow a=\dfrac{4}{3}\)

⇒ \(C(\dfrac{4}{3};\dfrac{4}{3})\) là điểm cần tìm.