Tìm min hoặc max của 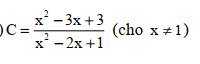

Những câu hỏi liên quan
Tìm min hoặc max của Q= 12x+34 / x2+2
Ta có: \(Q=\frac{12x+34}{x^2+2}\)
Đặt A=Q
=>\(12x+34=A\left(x^2+2\right)\)
=>\(A\cdot x^2+2A-12x-34=0\)
=>\(A\cdot x^2-12x+2A-34=0\) (1)
\(\Delta=\left(-12\right)^2-4A\left(2A-34\right)\)
\(=144-8A^2+136A=-8\left(A^2-17A-18\right)\)
\(=-8\left(A-18\right)\left(A+1\right)\)
Để (1) có nghiệm thì Δ>=0
=>-8(A-18)(A+1)>=0
=>(A-18)(A+1)<=0
=>-1<=A<=18
hay -1<=Q<=18
Do đó, ta có:
Giá trị lớn nhất của Q là 18 khi \(\frac{12x+34}{x^2+2}=18\)
=>\(18\left(x^2+2\right)=12x+34\)
=>\(9\cdot\left(x^2+2\right)=6x+17\)
=>\(9x^2+18-6x-17=0\)
=>\(9x^2-6x+1=0\)
=>\(\left(3x-1\right)^2=0\)
=>3x-1=0
=>\(x=\frac13\)
Giá trị nhỏ nhất của Q là -1 khi \(\frac{12x+34}{x^2+2}=-1\)
=>\(x^2+2=-12x-34\)
=>\(x^2+12x+36=0\)
=>\(\left(x+6\right)^2=0\)
=>x+6=0
=>x=-6
Đúng 0
Bình luận (0)
tìm min hoặc max của 2x2+x
tìm min hoặc max của 2x2 +x
Bài này tìm được min thôi
Ta có: \(2x^2+x=2\left(x^2+\frac{1}{2}x+\frac{1}{16}\right)-\frac{1}{8}=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)
Vậy Min = -1/8 khi x = -1/4
tìm Max hoặc Min của biểu thức:
D=21/|x-2|+3
E=1-x ²/x ²+5
\(D=\dfrac{21}{\left|x-2\right|+3}\le\dfrac{21}{3}=7\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (1)
Tìm Min hoặc Max của
C = 2x^2 + y^2 - 2xy - 2y + 5
\(C=2x^2+y^2-2xy-2y+5\)
\(\Rightarrow2C=4x^2+2y^2-4xy-4y-10\)
\(2C=\left(2x\right)^2-2.2x.y+y^2+y^2-4y+4-14\)
\(2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\)
Với mọi x, y ta có: \(\left(2x-y\right)^2\ge0;\left(y-2\right)^2\ge0\)
\(\Rightarrow\left(2x-y\right)^2+\left(y-2\right)^2\ge0\)
\(\Rightarrow2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\ge-14\)
\(\Rightarrow C\ge\frac{-14}{2}=-7\)
Dấu bằng xảy ra khi: \(\hept{\begin{cases}2x-y=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x=y\\y=2\end{cases}\Leftrightarrow}\hept{\begin{cases}2x=2\\y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}}\)
Vậy x=1 ; y=2 thì min C = -7
HỌC TỐT <3
Đúng 0
Bình luận (0)
Tìm Min hoặc Max
\(F=\sqrt{-3x^2-6x+2}\)
\(F=\sqrt{-3x^2-6x+2}\left(Đk:-1-\sqrt{\dfrac{5}{3}}\le x\le\sqrt{\dfrac{5}{3}}-1\right)\)
\(=\sqrt{-\left(3x^2+6x+3\right)+5}\)
\(=\sqrt{-3\left(x+1\right)^2+5}\)
Vì \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow F\le\sqrt{5}\)
\(MaxF=\sqrt{5}\Leftrightarrow x=-1\)
Đúng 3
Bình luận (1)
tìm max hoặc min `D= -10 - (x-3)² - |y-5|`
Ta có: \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y-5\right|\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-3\right)^2+\left|y-5\right|\ge0\forall x,y\)
\(\Rightarrow10+\left(x-3\right)^2+\left|y-5\right|\ge10\forall x,y\)
\(\Rightarrow D=-10-\left(x-3\right)^2-\left|y-5\right|\le-10\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x-3=0\\y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=5\end{matrix}\right.\)
Vậy \(Max_D=-10\) khi \(x=3;y=5\).
Đúng 3
Bình luận (0)
Tìm min hoặc max
|x-3|+|x-5|+|x+2|-4
\(A=\left|x-3\right|+\left|5-x\right|+\left|x+2\right|-4\ge\left|x-3\right|+\left|5-x+x+2\right|-4\)
\(A\ge\left|x-3\right|+3\ge3\)
\(A_{min}=3\) khi \(x=3\)
Đúng 1
Bình luận (0)
tìm min hoặc max `A = (x+3)^4 + (x-7)^4`
Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)
Áp dụng:
\(A=\left(x+3\right)^4+\left(7-x\right)^4\ge\dfrac{1}{2}\left[\left(x+3\right)^2+\left(7-x\right)^2\right]^2\)
Tiếp tục áp dụng BĐT ban đầu trong 2 số hạng trong ngoặc vuông:
\(\Rightarrow A\ge\dfrac{1}{2}\left[\dfrac{1}{2}\left(x+3+7-x\right)^2\right]^2=1250\)
Dấu "=" xảy ra khi \(x+3=7-x\Rightarrow x=2\)
Vậy \(A_{min}=1250\) khi \(x=2\)
Không tồn tại A max
Đúng 2
Bình luận (0)













