Dạ Em chào Thầy/Cô ạ!
Dạ Thầy/Cô giúp em giải bài này với ạ !
Em xin cảm ơn ạ

Dạ em chào Thầy/Cô,
Thầy/Cô giải giúp em Câu 3 với ạ
Em cảm ơn nhiều ạ

1, VTCP \(\overrightarrow{AC}=\left(-2;2\right)\); A(4;3)
PTTS : \(\left\{{}\begin{matrix}x=4+2t\\y=3-2t\end{matrix}\right.\)( t là tham số )
VTPT ( -2;-2) ; A(4;3)
PTTQ : \(-2\left(x-4\right)-2\left(y-3\right)=0\Leftrightarrow-2x-2y+14=0\Leftrightarrow x+y-7=0\)
2, AB : \(VTCP\overrightarrow{AB}=\left(-10;-2\right)\)
Do delta vuông góc với AB nên VTCP AB là VTPT đt delta
delta \(-10\left(x-2\right)-2\left(y-5\right)=0\Leftrightarrow-10x-2y+30=0\Leftrightarrow5x+y-15=0\)
3, pt đường tròn có dạng \(\left(x+6\right)^2+\left(y-1\right)^2=R^2\)
do pt (C1) thuộc A nên \(\left(4+6\right)^2+\left(3-1\right)^2=R^2\Leftrightarrow104=R^2\)
=> \(\left(C1\right):\left(x+6\right)^2+\left(y-1\right)^2=104\)
4, tâm \(I\left(3;4\right)\)
\(R=\dfrac{AC}{2}=\dfrac{\sqrt{4+4}}{2}=\dfrac{\sqrt{8}}{2}\Rightarrow R^2=2\)
\(\left(C2\right):\left(x-3\right)^2+\left(y-4\right)^2=2\)
Dạ Thầy cô giải giúp em câu này với ạ
Em Cảm ơn nhiều ạ

1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp
Dạ thầy cô giải giúp em 2 câu theo cách trong sách với ạ
Dạ em cảm ơn nhiều ạ

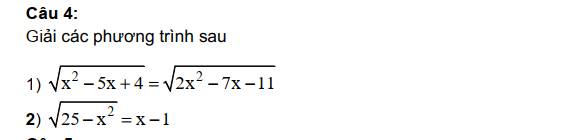
1: =>2x^2-7x-11=x^2-5x+4
=>x^2-2x-15=0
=>(x-5)(x+3)=0
=>x=5 hoặc x=-3
2: =>x>=1 và 25-x^2=x^2-2x+1
=>x^2-2x+1-25+x^2=0 và x>=1
=>2x^2-2x-24=0 và x>=1
=>x=4
1.
Bình phương hai vế pt đã cho ta được:
\(x^2-5x+4=2x^2-7x-11\)
\(\Rightarrow x^2-2x-15=0\)
\(\Rightarrow x=5\) hoặc \(x=-3\)
Thay lần lượt hai giá trị trên vào pt đã cho ta thấy đều thỏa mãn
Vậy nghiệm của pt là \(S=\left\{-3;5\right\}\)
2.
Bình phương 2 vế pt đã cho:
\(25-x^2=\left(x-1\right)^2\)
\(\Rightarrow25-x^2=x^2-2x-1\)
\(\Rightarrow2x^2-2x-24=0\)
\(\Rightarrow x=4\) hoặc \(x=-3\)
Lần lượt thay các giá trị trên vào pt đã cho ta thấy chỉ có \(x=4\) thỏa mãn
Vậy nghiệm của pt đã cho là \(S=\left\{4\right\}\)
Dạ con nhờ thầy cô giải giúp con bài này với ạ.
Một khối học sinh khi xếp 4 hàng,5 hàng,6 hàng đến thiếu 2 em.Biết số học sinh chưa đến 300 em.Tính số học sinh của khối đó.
Dạ em xin cảm ơn ạ.
Olm chào em. Cảm ơn em đã tin tưởng và đồng hành cùng olm trong suốt thời gian qua. Với dạng này em làm như sau nhé:
Gọi số học sinh của khối đó là \(x\) (học sinh) 0 < \(x\) < 300; \(x\) \(\in\) N
Theo bài ra ta có: ( \(x\) + 2) \(⋮\) 4; 5; 6
⇒ (\(x\) + 2) \(\in\) BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< \(x\) < 300 ⇒0< \(x\) + 2 < 300 + 2 ⇒ 2 < \(x\) + 2 < 302
⇒ \(x\) + 2 \(\in\){60; 120; 180; 240; 300}
Lập bảng ta có:
| \(x+2\) | 60 | 120 | 180 | 240 | 300 |
| \(x\) | 58 | 118 | 178 | 238 | 298 |
Vậy \(x\) \(\in\){58; 118; 178; 238; 298}
Gọi số học sinh của khối đó là (học sinh) 0 < < 300; N
Theo bài ra ta có: ( + 2) 4; 5; 6
⇒ ( + 2) BC(4; 5; 6)
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5;6) = 22.3.5 = 60
⇒ BC(4;5;6) = {0; 60; 120; 180; 240; 300; 360; 420; ...;}
Vì 0< < 300 ⇒0< + 2 < 300 + 2 ⇒ 2 < + 2 < 302
⇒ + 2 {60; 120; 180; 240; 300}
Lập bảng ta có:
| 60 | 120 | 180 | 240 | 300 | |
| 58 | 118 | 178 | 238 | 298 |
Vậy {58; 118; 178; 238; 298}
Dạ thầy cô có đề tuần 1 tiếng anh lớp 5 cho em xin với ạ! Em cảm ơn các bạn, các thày cô olm!
Em vào học bài chọn lớp,chọn môn chọn đề rồi tải em nhá
Tìm a,b,c biết:
4abc : abc = 26
Dạ!Mong thầy cô và các bạn giúp em giải bài toán này ạ!!!!!Em xin cảm ơn
Ta có:
4abc:abc=26
(4000+abc):abc=26
4000+abc=abcx26
4000=(abcX 26)-abc
4000=25 x abc
abc=4000:25
abc=160
Chúc Hà học giỏi ,nhớ k cho mình nữa nha!
Dạ Thầy Cô giải giúp em câu này với ạ
Em không chắc chắn lắm !![]()

1: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-4}{2}=-2\\y=-\dfrac{4^2-4\cdot1\cdot\left(-5\right)}{4}=-9\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) -2 +\(\infty\) |
| y | -\(\infty\) -9 +\(\infty\) |
2:
a: Hàm số đồng biến khi x>-2 và nghịch biến khi x<-2
b: Hàm số ko có giá trị lớn nhất
y=x^2+4x-5
=(x+2)^2-9>=-9
Dấu = xảy ra khi x=-2
Dạ thầy cô và các bạn giúp em cách làm câu 6a với ạ.
Em cảm ơn
\(y'=\left(m+3\right)x^2-4x+m\)
Hàm nghịch biến trên R khi và chỉ khi \(y'\le0\) ; \(\forall x\in R\)
- Với \(m=-3\) ko thỏa mãn
- Với \(m\ne-3\) bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}m+3< 0\\\Delta'=4-m\left(m+3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -3\\\left[{}\begin{matrix}m\ge1\\m\le-4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow m\le-4\)
Dạ thầy cô và các bạn chỉ em câu a4,4b,4c,4d và câu 5a với ạ
Em cảm ơn ạ
4a.
\(y'=\dfrac{1}{cos^2x}+cosx-2=\dfrac{cos^3x-2cos^2x+1}{cos^2x}=\dfrac{\left(1-cosx\right)\left(1+cosx\left(1-cosx\right)\right)}{cos^2x}>0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm đồng biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4b.
\(y'=-sinx-1\le0\) ; \(\forall x\in\left(0;2\pi\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;2\pi\right)\)
c.
\(y'=-sinx-\dfrac{1}{sin^2x}+2=\dfrac{-sin^3x+2sin^2x-1}{sin^2x}=\dfrac{\left(sinx-1\right)\left(1-sin^2x+sinx\right)}{sin^2x}\)
\(=\dfrac{\left(sinx-1\right)\left(cos^2x+sinx\right)}{sin^2x}< 0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4d.
\(y=cosx+sinx.cosx=cosx+\dfrac{1}{2}sin2x\)
\(y'=-sinx+cos2x=-sinx+1-2sin^2x\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{3\pi}{2}\right\}\)
Bảng biến thiên
Từ BBt ta thấy hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{5\pi}{6};2\pi\right)\)
Hàm nghịch biến trên \(\left(\dfrac{\pi}{6};\dfrac{5\pi}{6}\right)\)
5a.
\(y'=x^2-4x+m\)
Hàm đồng biến trên TXĐ khi và chỉ khi \(y'\ge0\) ; \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=4-m\le0\end{matrix}\right.\)
\(\Leftrightarrow m\ge4\)