Một xe tải có chiều rộng 2,4m và chiều cao là 2,5m muốn đi qua một cái cổng có hình Parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng (đỉnh Parabol) tới chân cổng là 2\(\sqrt{5}\) m (bỏ qua độ dày của cổng).

a, Trong mặt phẳng tọa độ Oxy, gọi Parabol (P): y=ax\(^2\) với a>0 là hình chiếu biểu diễn cổng mà xe tải muốn đi qua . Chứng minh a=-1

b, Hỏi xe tải có đi qua cổng được không ? Tại sao?

Hình vẽ bên dưới mô tả đoạn đường đi vào GARA ôtô nhà cô Hiền. Đoạn đường đầu tiên có chiều rộng bằng x (m), đoạn đường thẳng vào cổng GARA có chiều rộng 2,6 (m). Biết kích thước xe ôtô là 5m × 1,9m (chiều dài × chiều rộng). Để tính toán và thiết kế đường đi cho ôtô người ta coi ôtô như một khối hộp chữ nhật có kích thước chiều dài 5 m, chiều rộng 1,9 m. Hỏi chiều rộng nhỏ nhất của đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị sau để ôtô có thể đi vào GARA được? (giả thiết ôtô không đi ra ngoài đường, không đi nghiêng và ôtô không bị biến dạng).

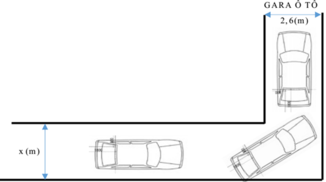
A. x = 3,55 (m).

B. x = 2,6 (m).

C. x = 4,27 (m).

D. x = 3,7 (m).

Khi đang lái xe qua một ngọn núi, nhóm tài xế phải dừng lại do tảng đá rơi xuống, chắn lối vào hầm.

Một số người xuống xe để di dời tảng đá. Tuy nhiên, khi lối vào hầm đã thông thoáng, vấn đề khác lại xuất hiện khi phía sau họ là hàng dài xe dừng lại vì tắc đường.

Tình trạng tắc nghẽn trên con đường có hai làn này do 18 chiếc xe màu trắng và 18 chiếc xe màu đen gây ra. Chiếc đầu tiên nằm ở làn bên trái màu trắng trong khi chiếc đầu tiên nằm trên làn phải màu đen.

Những chiếc xe kế tiếp có màu sắc xen kẽ (như vậy, làn bên trái sẽ là trắng - đen - trắng..., làn bên phải là đen - trắng - đen...).

Đi qua đường hầm chật hẹp, hai làn xe phải hợp lại thành một và khi đi hết đoạn đường hầm, các xe lại tách làm hai nhánh để đi qua trạm thu phí.

Giả sử chiếc xe đầu tiên ra khỏi đường hầm có màu đen, chiếc cuối cùng có màu trắng và các xe đi qua trạm thu phí thành từng cặp (hai xe đi đầu cùng qua trạm tại một thời điểm rồi lại đến hai xe tiếp theo).

Như vậy, tối đa có bao nhiêu cặp xe có màu giống nhau cùng qua trạm?

Hình vẽ bên dưới mô tả đoạn đường đi vào GARA Ô TÔ nhà cô Hiền. Đoạn đường đầu tiên có chiều rộng bằng x(m), đoạn đường thẳng vào cổng GARA có chiều rộng 2,6(m). Biết kích thước xe ô tô là 5m x 1,9m (chiều dài x chiều rộng). Để tính toán và thiết kế đường đi cho ô tô người ta coi ô tô như một khối hộp chữ nhật có kích thước chiều dài bằng 5m, chiều rộng 1,9m. Hỏi chiều rộng nhỉ nhất của đoạn đường đầu tiên gần nhất với giá trị nào trong các giá trị bên dưới để ô tô có thể đi vào GARA được ? (giả thiết ô tô không đi ra ngoài đường, không đi nghiêng và ô tô không bị biến dạng).

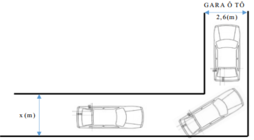
A. x = 3,7(m)

B. x = 3,55(m)

C. x = 4,27(m)

C. x = 4,27(m)

Một xe tải có chiều rộng là 2,4m chiều cao là 2,5 m muốn đi qua cổng hình parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh đến mỗi chân cổng là 2 căn 5 m

a/ Trong mp tọa độ Oxy gọi parabol (P): y = ax² với a <0 là hình biểu diễn cổng mà xe tải muốn đi qua. Chứng minh a = -1

b/ Hỏi xe tải đi qua cổng được không? Tại sao?

@Akai Haruma

khi du lịch đến thành phố Xanh lu-i ( Mỹ ) ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới , đó là cổng Ac - xơ. Gỉa sử ta lập một hệ tọa độ Oxy sao cho chân cổng đi qua gốc O ( x,y tính bằng mét ) , chân kia của cỏng ở vị trí ( 162;0 ) . biết một điểm M trên cổng có tọa độ là ( 10;43 ) :  a) tìm hàm số bậc 2 có đồ thị chứa cung parabol nói trên  ;  b) tính chiều cao của cổng ( tính từ điểm cao nhất trên cổng xuống mặt đất , làm tròn kết quả đến hàng đơn vị )