Những câu hỏi liên quan
Trong các độ dài sau, ba số đo nào là số đo ba cạnh của một tam giác vuông?
a) 2cm; 2cm; 2✓2cm
b) 8cm; 15cm; 17cm
c) 24cm; 7cm; 25cm
d) 6cm; 8cm; 10cm
e) 6cm; 9cm; 11cm
f) 1cm; 1cm; 3/2cm
Xem chi tiết
Bạn cho mình hỏi chỗ :2√2 là j ạ
Đúng 0
Bình luận (2)
a) Ta có: \(\left(2\sqrt{2}\right)^2=8\)
\(2^2+2^2=4+4=8\)
Do đó: \(\left(2\sqrt{2}\right)^2=2^2+2^2\)(=8)
hay \(2\sqrt{2}\)cm; 2cm; 2cm là số đo ba cạnh của một tam giác vuông
b) Ta có: \(17^2=289\)
\(8^2+15^2=64+225=289\)
Do đó: \(17^2=8^2+15^2\)(=289)
hay 17cm; 8cm và 15cm là số đo ba cạnh của một tam giác vuông
c) Ta có: \(25^2=625\)
\(7^2+24^2=49+576=625\)
Do đó: \(25^2=7^2+24^2\)(=625)
hay 25cm; 7cm và 24cm là số đo ba cạnh của một tam giác vuông
d) Ta có: \(10^2=100\)
\(6^2+8^2=36+64=100\)
Do đó: \(10^2=6^2+8^2\)(=100)
hay 10cm; 6cm và 8cm là số đo ba cạnh của một tam giác vuông
e) Ta có: \(11^2=121\)
\(6^2+9^2=36+81=117\)
Do đó: \(11^2\ne6^2+9^2\)(\(121\ne117\))
hay 11cm; 6cm và 9cm không là số đo ba cạnh của một tam giác vuông
f) Ta có: \(\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(1^2+1^2=1+1=2=\dfrac{8}{4}\)
Do đó: \(\left(\dfrac{3}{2}\right)^2\ne1^2+1^2\left(\dfrac{9}{4}\ne\dfrac{8}{4}\right)\)
hay \(\dfrac{3}{2}cm\); 1cm và 1cm không là số đo ba cạnh của một tam giác vuông
Đúng 2
Bình luận (0)
A B C D E F G H 12 cm y 16 cm Hình vẽ bên, cho biết: AB // CD // EF // GH; AC CE EG;BD DF FH; AB x(cm); CD 12cm; EF y(cm); GH 16cm.Thế thì giá trị của x và y là:
Đọc tiếp
Hình vẽ bên, cho biết: AB // CD // EF // GH; AC = CE = EG;
BD = DF = FH; AB = x(cm); CD = 12cm; EF = y(cm); GH = 16cm.
Thế thì giá trị của x và y là:
Giải:
Hình thang CDHG có: CE = GE , DF = HF ( gt )
=> EF là đường TB của hình thang.
=> EF = \(\dfrac{CD+GH}{2}\) = \(\dfrac{12+16}{2}\) = 14 cm ( hay y = 14 cm )
Hình thang ABFE có: AC = CE, BD = DF ( gt )
=> CD là đường TB của hình thang trên.
=> CD = \(\dfrac{AB+EF}{2}\)
mà CD = 12 cm, EF = 14 cm ( cmt )
=> AB = 12.2 - 14 = 10 cm ( hay x = 10 cm )
Vậy x = 10 cm, y = 14 cm
Đúng 0
Bình luận (0)
*Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC= 6cm. Gọi E, F lần lượt là hình chiếu của AH trên cạnh AB, AC.
a. Tính độ dài AC và tìm số đo góc B và C.
b. Tính độ dài AH và chứng minh EF=AH.
c. Tính EA.EB + FA.FC.
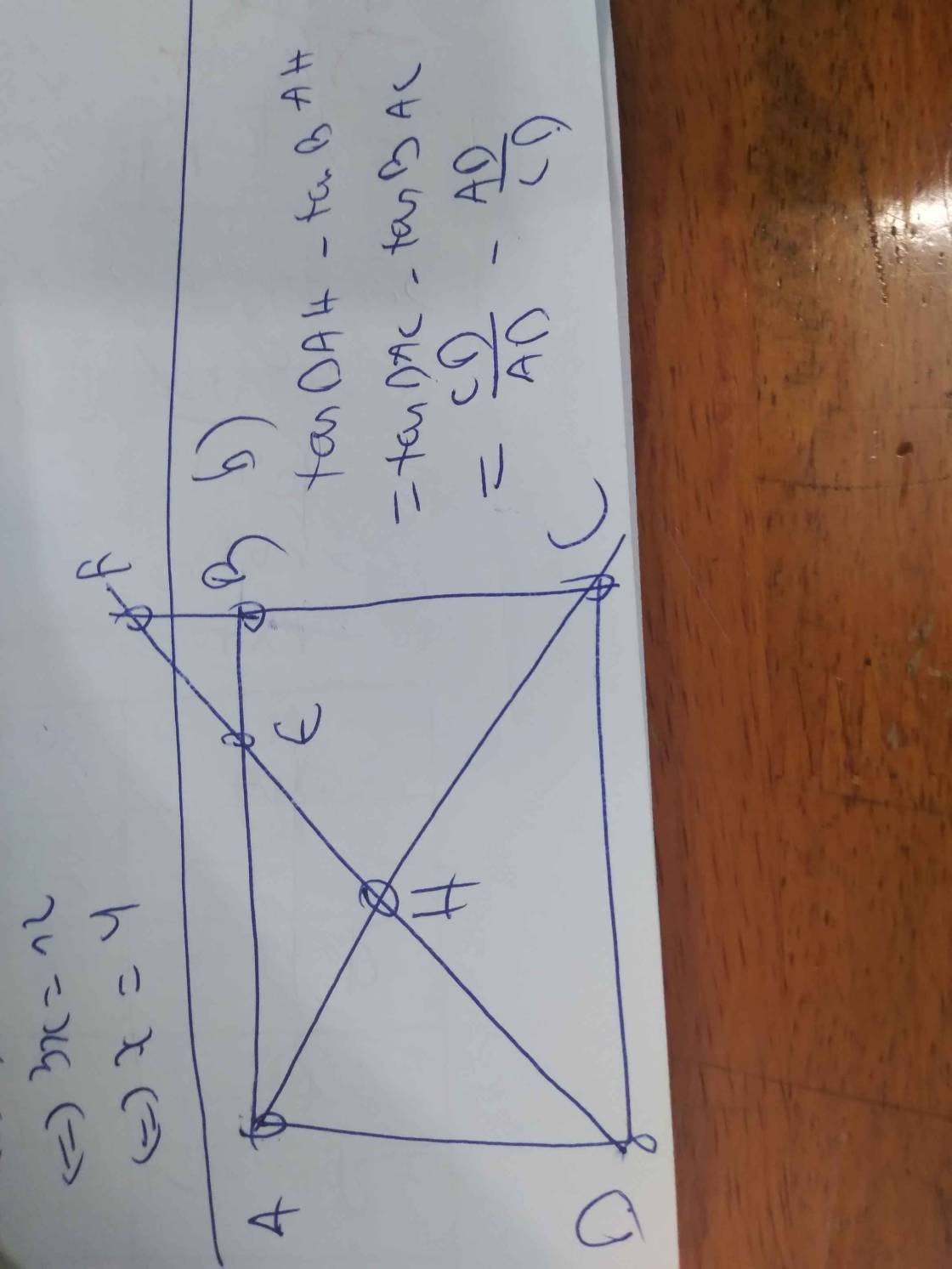
Vẽ hình chữ nhật ABCD ( biết AB>AD) có DH vuông góc AC tại H.
a) Biết AB = 6cm. AH = 3,6 cm. Tính AC và BA?
b) Kéo DH cắt AB tại E và BC tại F. Cm: EF/AC = tanDAH - tanBAH
Mình cần câu b ạ, không hình cũng được ạ. mình cảm ơn
Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Lấy trên cạnh AB, AC lần lượt các điểm E, F sao cho AE = 1,5cm và AF = 2cm.
a) CMR: EF // BC
b) Tính EF?
c) Gọi EC giao FB tại K. CMR: KE. KB = KF. KC
a) Ta có :
\(\frac{AE}{AB}=\frac{1,5}{6}=\frac{1}{4}\)
\(\frac{AF}{AC}=\frac{2}{8}=\frac{1}{4}\)
\(\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}\)
\(\Rightarrow EF//BC\)(Theo định lí Ta-lét đảo)
b)Áp dụng định lí Pythagoras vào △ABC vuông tại A :
BC2 = AB2 + AC2
\(\Rightarrow\)BC2 = 62 + 82
\(\Rightarrow\)BC2 = 100
\(\Rightarrow\)BC = 10 cm
Xét △ABC có : MN // BC
\(\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}=\frac{EF}{BC}\)(Hệ quả định lí Ta-lét)
\(\Rightarrow\frac{EF}{BC}=\frac{1}{4}\)
\(\Rightarrow EF=\frac{1}{4}BC=\frac{1}{4}\cdot10=2,5\left(cm\right)\)
c) Xét △KBC có EF // BC
\(\Rightarrow\frac{KB}{KF}=\frac{KC}{KE}\)(Theo định lí Ta-lét)
\(\Rightarrow KE.KB=KF.KC\)
Cho ∆ABC có EF // BC (E thuộc AB, F thuộc AC), đường phân giác AD cắt BC tại D, biết AE = 6cm, EB = 3cm, FC = 4cm, DC = 6cm. AF = x, BD = y, EF = z a) Tính x, y b) Tính z
a) Áp dụng định lý Ta-let vào \(\Delta\)ABC, ta có:
\(\frac{AE}{BE}=\frac{AF}{FC}\)
\(\rightarrow\frac{6}{3}=\frac{x}{4}\)
\(\rightarrow x=8\)
Gọi AD là a, ta có:
\(\frac{AF}{FC}=\frac{AD}{DC}\)
\(\rightarrow\frac{6}{3}=\frac{a}{6}\)
\(\rightarrow a=12\)
Vậy:
\(\frac{AE}{BE}=\frac{AD}{BD}\)
\(\rightarrow\frac{6}{3}=\frac{12}{y}\)
\(\rightarrow y=6\)
Áp dụng hệ quả TaLet vào \(\Delta\)ABC, ta có:
\(\frac{EF}{BC}=\frac{AE}{BE}\)
\(\rightarrow\frac{z}{12}=\frac{6}{3}\)
\(\rightarrow z=24\)
1.Cho hình thang cân ABCD(AB//CD), góc BDC=45o. Gọi O là giao điểm của AC và BD.
a. CM tam giác DOC vuông cân
b. Tính diện tích của hình thang ABCD, biết BD=6cm
2. a. Tìm x của tứ giác ABCD, biết góc A=60 độ, góc C= 90 độ, góc D=63 độ
b. Cho hình thang ABCD(AB//CD). E,F lần lượt là trung điểm AD, BC. Tính độ dài đoạn thẳng EF, biết AB=3cm,CD=9cm
Câu 3: Cho tam giác nhọn ABC có AB = 6cm , AC = 9 cm. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 2cm, AE = 3cm.
a, Chứng minh rằng : Tam giác ADE đồng dạng Tam giác ABC?
b, Từ E kẻ EF // AB (F thuộc BC ). Tính tỉ số chu vi của Tam giác EFC và Tam giác ADE ?
a) Xét tam giác ADE và tam giác ABC có:
\(\widehat{A}\): góc chung
\(\frac{AD}{AB}=\frac{AE}{AC}\left(\frac{2}{6}=\frac{3}{9}=\frac{1}{3}\right)\)
=>\(\Delta ADE\) đồng dạng với \(\Delta ABC\) (c-g-c)
b)Xét tam giác ABC có EF//AB
=> \(\Delta CEF\) đồng dạng với \(\Delta CAB\)
Ta có : EC=CA-AE=9-3=6
=>\(\frac{CE}{CA}=\frac{CF}{CB}=\frac{EF}{AB}=\frac{6}{9}=\frac{2}{3}\)
Vì \(\Delta ADE\) đồng dạng với \(\Delta ABC\)
=>\(\frac{S_{ADE}}{S_{ABC}}=\frac{AE}{AC}=\frac{1}{3}\) (1)
Vì \(\Delta CEF\) đồng dạng với \(\Delta CAB\)
=>\(\frac{S_{EFC}}{S_{ABC}}=\frac{EC}{AC}=\frac{2}{3}\) (2)
Từ (1) và (2) =>\(\frac{S_{ADE}}{S_{EFC}}=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 10cm. Trên cạnh AB lấy điểm D sao cho BD = 2cm. Kẻ DE vuông góc AB ( E thuộc BC). Gọi F là hình chiếu của E trên AC.
1.Cm DF = AE
2. Trên tia FC lấy Q sao cho FQ = DE. Gọi Mlaf giao điểm của DQ và EF. Gọi O là giao điểm AE và DF . Cm OM // AC.
3. Vẽ G sao cho E và C đối xứng với nhau qua G . tính S tam giác OEG